Test #f# for concavity?
#f# 2 times differentiable in #RR# with:
#(f'(x))^3+3f'(x)=e^x+cosx+x^3+2x+7#
#AA# #x# #in# #RR#
2 Answers
Explanation:
Solved it i think.
We have
Differentiating both parts we get
#f'(x)^2>=0# so#f'(x)^2+1>0#
We need the sign of the numerator so we consider a new function
,
We notice that
For
For
We finally get this table which shows the monotony of
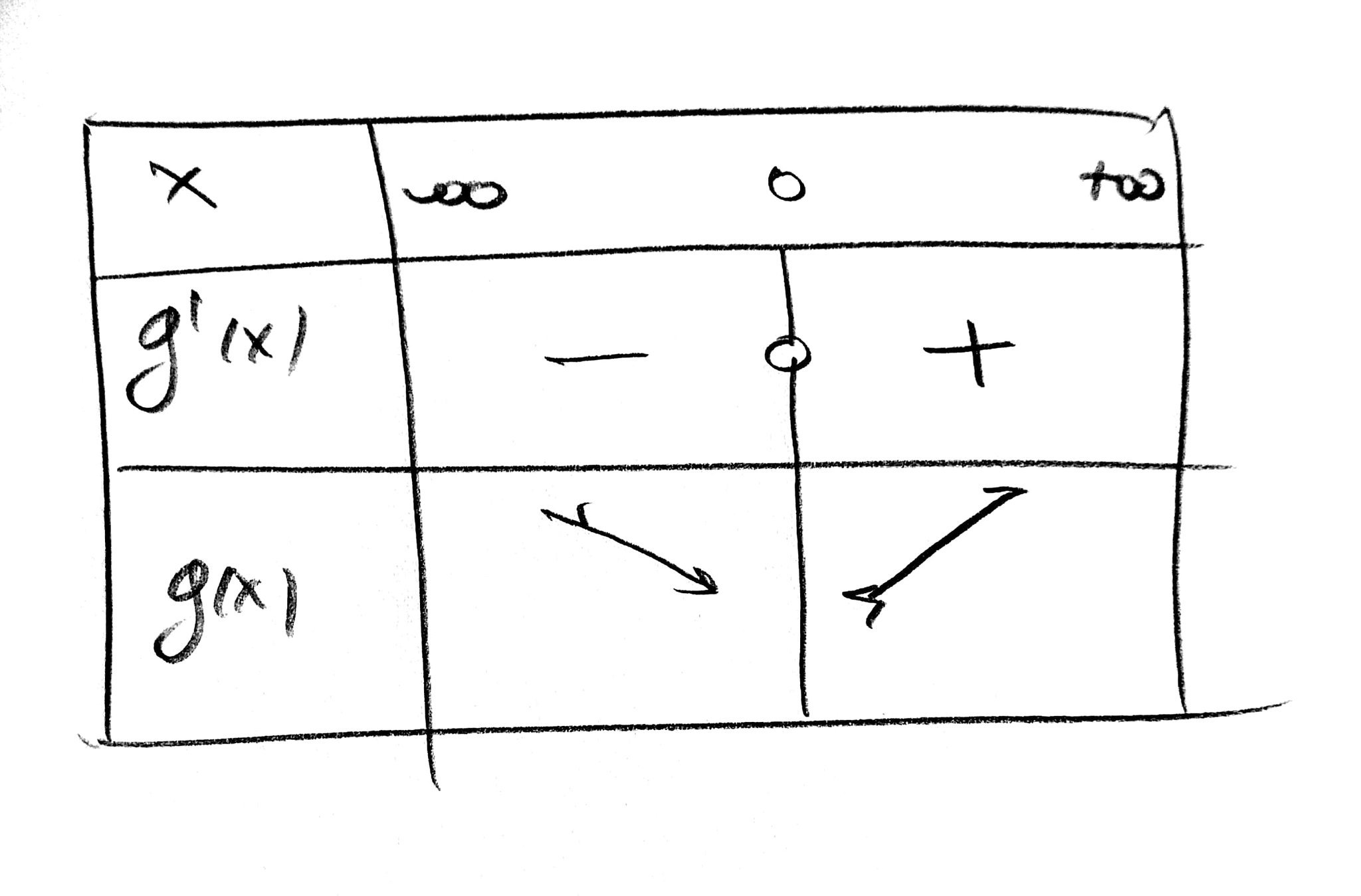
Supposed
because
#lim_(xrarr-oo)g(x)=lim_(xrarr-oo)(e^x-sinx+3x^2+2)#
- Using the squeeze/sandwich theorem we have
Therefore,
#lim_(xrarr+oo)g(x)=lim_(xrarr+oo)(e^x-sinx+3x^2+2)#
With the same process we end up to
However,
Therefore,
The range of
#0!inR_g=[3,+oo)# so#g# has no roots in#RR#
#g# is continuous in#RR# and has no solutions. Therefore,#g# preserves sign in#RR#
That means
Thus,
As a result
And
See below.
Explanation:
Given
now analyzing


