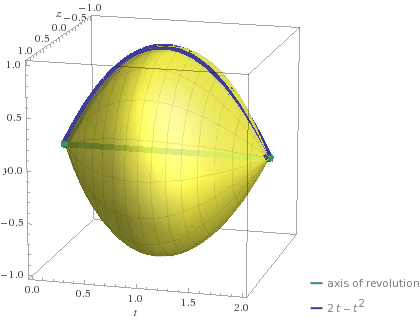
The area bounded by the curve y=3+2x-x^2 and line y=3 is rotated completely about the line y=3. Find the volume of the solid of revolution obtained?
1 Answer
Explanation:
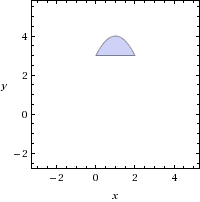
The area are the solution of this system:
And it is sketched in this plot:
The formula for the volume of a x-axis rotation solid is:
To apply the formula we should translate the half moon on the x-axis, the area won't change, and so it won't change also the volume:
In this way we obtain
The translated area now is plotted here:
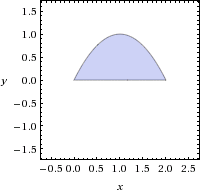
But which are the a and b of the integral? The solutions of the system:
So
Let's rewrite and solve the integral:
And this "lemon" is the solid obtained: