Question

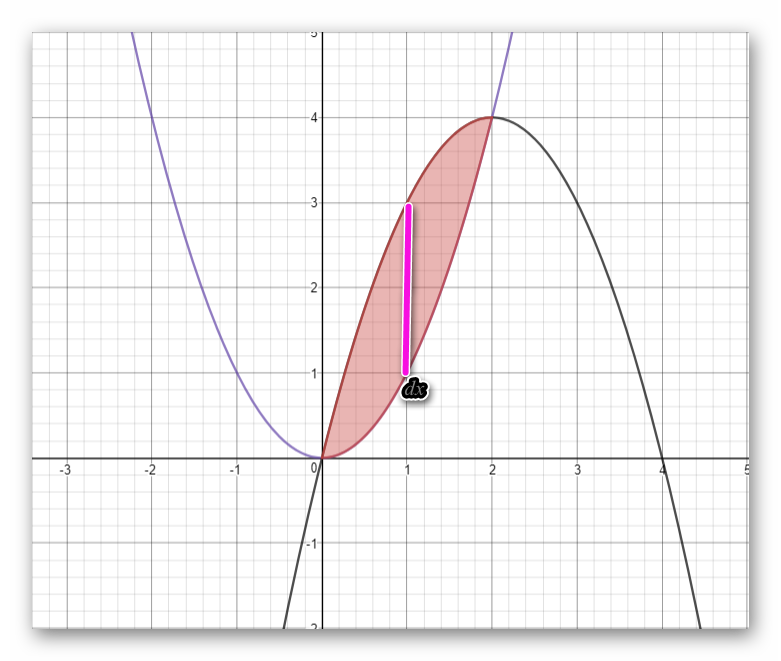
The area of the region bounded by the curve y=x^2 and y=4x-x^2 is ?

Answer 1

`color(blue)[A=int_0^2(4x-x^2)-(x^2)*dx=8/3=2.667 (unite)^2]`

Explanation:

Firstly lets find the limits of the Area

since `y=x^2` and `y=4x-x^2`

`x^2=4x-x^2`

`2x^2-4x=0 rArr 2x*(x-2)=0`

`2x=0 rArr x=0`

since `x=0 rArr y=x^2 rArr y=0`

`A=(0,0)`

`x-2=0 rArr x=2`

since `x=2 rArr y=x^2 rArr y=4`

`B=(2,4)`

if we take dx slice (that mean the Area revolving about x-axis)

The interval of the integral become

`x in [0,2]`

now let set up the integral of Area

`color(red)[A=int_a^by_2-y_1*dx`

`A=int_0^2(4x-x^2)-(x^2)*dx`

`A=int_0^(2)4x-2x^2*dx=[2x^2-2/3x^3]_0^2`

`[8-16/3]=(24-16)/3=8/3=2.667 (unite)^2`

show the graph of the area below: