The asteroid Ceres has a mass of #7*10^20# #kg# and a radius of #500# #km#. What is #g# on the surface of Ceres? How much would a #99# #kg# astronaut weigh on Ceres?

1 Answer
Tanish J.
Dec 30, 2015

#g=0.1868 m/s^2#

and the astronaut would weigh #18.4932N#

Explanation:

To solve this question, we'll first need to understand how we can arrive at the value of #g#.

From Newton's Universal Law of Gravitation, we have:

#F=G (Mm)/R^2#

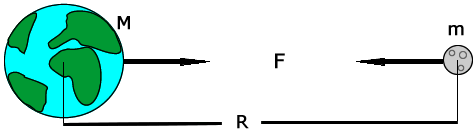
School for Champions

Where,

#F# is the force of attraction on the larger object by the smaller object OR the force of attraction on the smaller object by the larger object,

#G# is the universal gravitational constant, #=6.67408 × 10^-11 m^3 kg^-1 s^-2#,

#M# is the mass of the larger object,

#m# is the mass of the smaller object,

and #R# is the distance by which their centres of mass are separated.
(For a sphere, the centre of mass lies at its geometrical centre.)

But from Newton's Second Law, we have:

#F=ma#

Substituting this in the first equation, we have

#cancelma=G (Mcancelm)/R^2#

#a=GM/R^2#

For a system consisting of an object on a planet or natural satellite,

#a# is written as #g# (acceleration due to gravity)

and #R# is equal to the radius of the planet.

Since the radius of a planet is so huge, we can usually neglect small distances from it. The image looks more like this now:

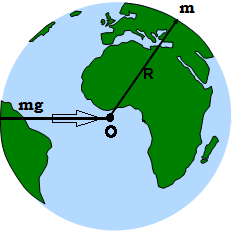
Merit Section

Alright, so we have reached on our final equation:

#g=GM/R^2#

It's interesting to notice that the value of #g# does not depend upon the mass of the smaller object #m#, which is why both heavy and small objects will accelerate towards a planet at equal rates. See Galileo's Leaning Tower of Pisa experiment .

Now, substituting the values we have for Ceres, we get:

#g=6.67408 × 10^-11 * (7*10^20)/(500*10^3)^2#

#g=1.868*10^-1 m/s^2#

or, #g=0.1868 m/s^2#

Now for the second part, we know that the weight of an object #(W)# is simply its mass #(m)# times the acceleration due to gravity #(g)#.

#W=mg#

Substituting the values we have,

#W=99*0.1868#

#W=18.4932N#

(You can compare this with #99*9.81=971.19N# on Earth.)

In case you want to know what a weighing scale from Earth would show in case the astronaut stepped on it on Ceres, you can divide his weight by #g_(earth)=9.81 m/s^2#,

which is #18.4932/9.81 = 1.8851 kg#

That's just what a weighing scale would show as we'd feel lighter on Ceres. The actual mass of the astronaut has not decreased!

Related questions
Impact of this question
32581 views around the world
You can reuse this answer
Creative Commons License