The base of an isosceles triangle is 3 cm longer than the equal sides, and 6 cm longer than the height of the triangle. Find the length of the triangle's base?

Question

2195 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-06-04T12:36:33

#color(blue)(6cm " or " 18cm)#

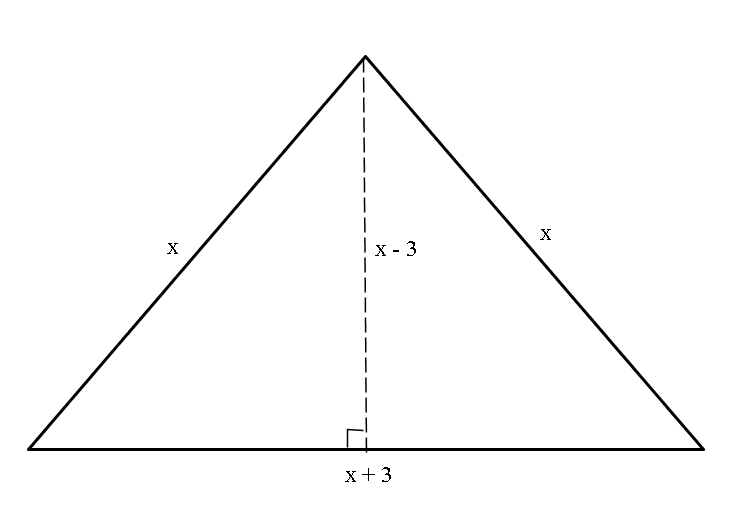
enter image source here

From the diagram:

Let the two equal sides be: #x#

Base is 3cm longer than the equal sides:

#"base"=x+3#

Height is 6 cm shorter than base:

#"height"=x+3-6=x-3#

Using Pythagoras' theorem:

#x^2=(x-3)^2+((x+3)/2)^2#

Expanding:

#x^2=5/4x^2-9/2x+45/4#

#x^2-5/4x^2+9/2x-45/4=0#

#4x^2-5x^2+18x-45=0#

#-x^2+18x-45=0#

Factor:

#(3-x)(x-15)=0=>x=15 and x=3#

Base of triangle is:

#x+3=>3+3=6#

or

#x+3=>15+3=18#