The coefficient of x^(-5)=?, in the binomial expansion of [((x+1)/((x^(2/3)-(x^(1/3))+1))-((x-1)/(x-(x^(1/2))]^10 , where 'x' not equal to 0,1 is:
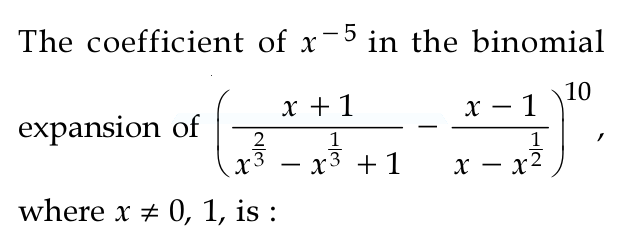
1 Answer
Feb 23, 2018
1
Explanation:
Since
Again
Thus the given expression simplifies to
The only way that we can get

