Question

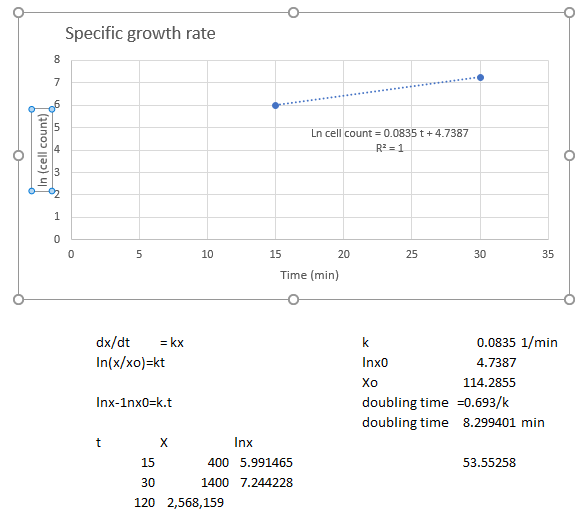
The count in a bacteria culture was 400 after 15 minutes and 1400 after 30 minutes. Assuming the count grows exponentially, initial size of the culture (rounded to 2 decimals)? doubling period.? population after 120 minutes? When population reach 10000?

Answer 1

X initial ~ 114.29; doubling time 8.3 min; after 120 min, 2,568,159 cells; 54 min, population reaches 10,000.

Explanation:

As the growth is exponential,
`dx/dt = kx`
Integrating, we get,
`lnx = lnx_0+kt`

The slope of the plot `ln(cell count)` against `t` in minutes would give the growth rate; the intercept will be ln(cellcount_initial).

~
From the graph, lnx0 = 4.7387
Thus xo= exp(4.7387)

~

k = 0.0835/min

~

Doubling time is related to k via the expression:
`t_d=0.693/k`

~

`t_d = 8.3 min`

~

`ln(x/x_o)=kt`
We know x_0, x is 10,000, k is known, time required to reach 10,000 can be calculated.

~ 54 min.