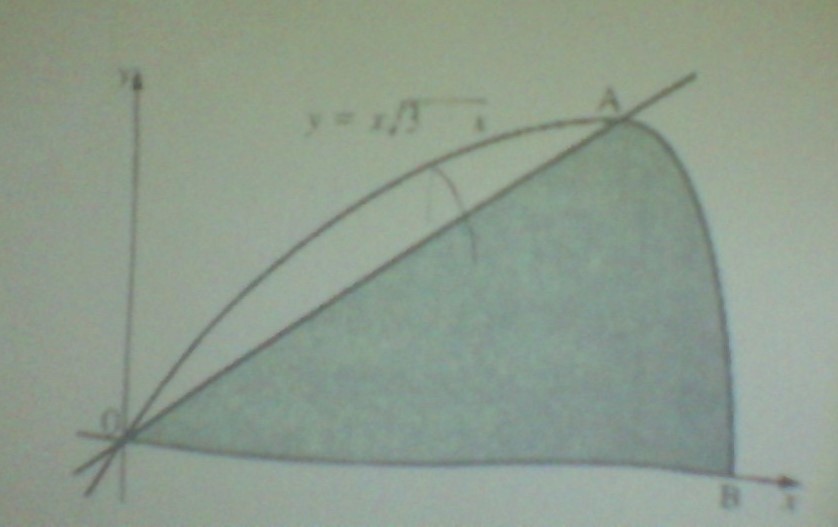
The curve with equation #y=x(3-x)^(1/2)# together with line segment OA.!) what are the coordinates of B and A; 2)what is the Area of the shaded region bounded by the line segment AO, x axis and the arc of AB curve?
1 Answer
The coordinates of
Explanation:
Calculation of the point
Let
Then,
The coordinates of
Calculation of the point
Calculate the derivative of
The maximum is when
That is
The point
The equation of the line
The area of the shaded region is
Calculation of
Let
Therefore,
Therefore, the area is
graph{(y-xsqrt(3-x))(y-x)=0 [-0.96, 5.197, -0.3, 2.778]}

