The equation of the curve is given by y=x^2+ax+3, where a is a constant. Given that this equation can also be written as y=(x+4)^2+b, find (1) the value of a and of b (2) the coordinates of the turning point of the curve Someone can help?
The equation of the curve is given by y=x^2+ax+3 , where a is a constant. Given that this equation can also be written as y=(x+4)^2+b , find
(1) the value of a and of b
(2) the coordinates of the turning point of the curve
The equation of the curve is given by
(1) the value of
(2) the coordinates of the turning point of the curve
2 Answers
The explanation is in the images.
Explanation:
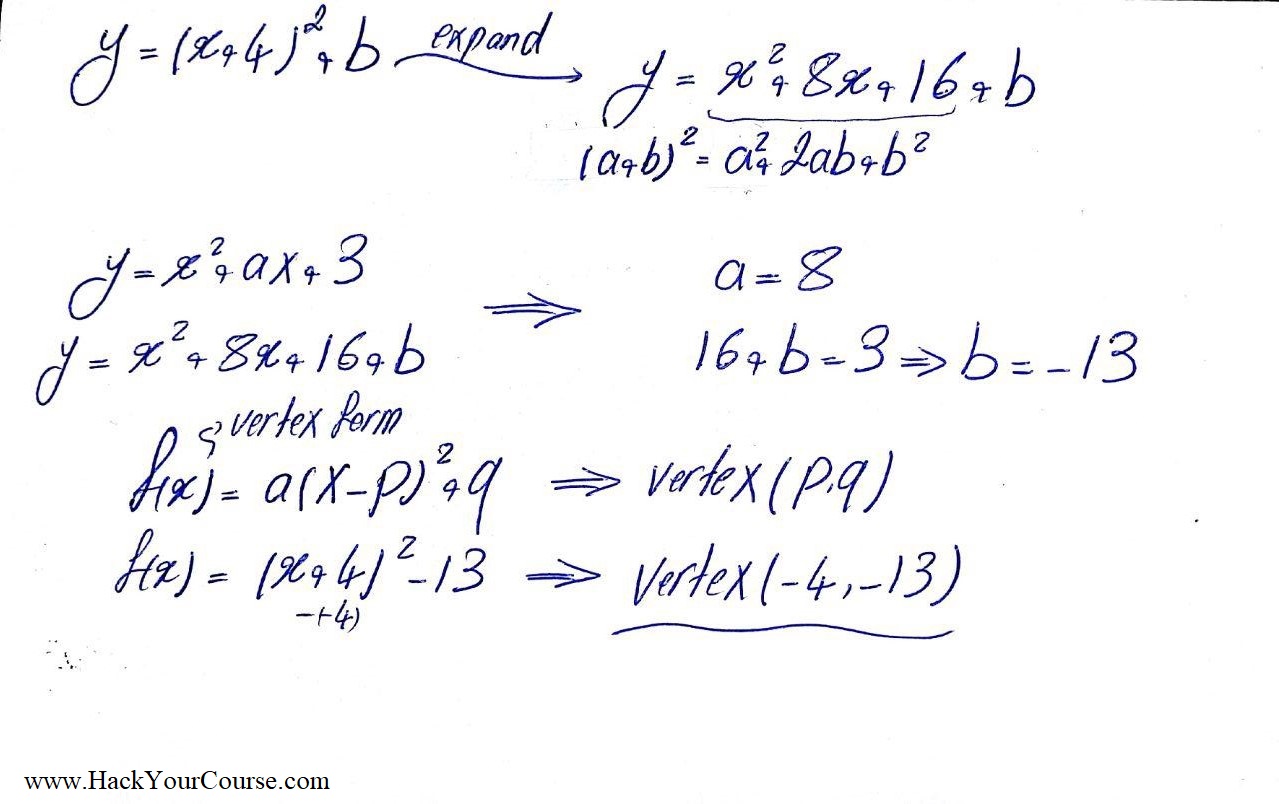
Explanation:
x^2+ax+3to(1)
y=(x+4)^2+bto(2)
"expanding "(2)" using FOIL"
y=x^2+8x+16+b
color(blue)"comparing coefficients of like terms"
ax-=8xrArra=8
16+b-=3rArrb=3-16=-13
"the equation of a parabola in "color(blue)"vertex form" is.
color(red)(bar(ul(|color(white)(2/2)color(black)(y=a(x-h)^2+k)color(white)(2/2)|)))
"where "(h,k)" are the coordinates of the vertex and a"
"is a multiplier"
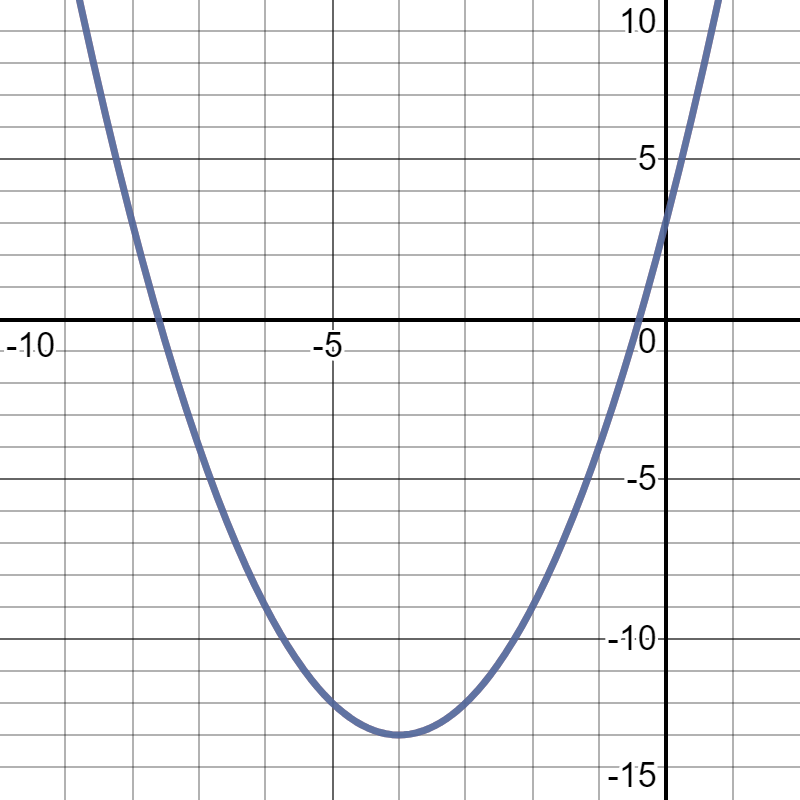
y=(x+4)^2-13color(blue)" is in vertex form"
rArrcolor(magenta)"vertex "=(-4,-13)larrcolor(blue)"turning point"


