.
#y=xsinx#
To find where the function is concave and where convex, we need to take the second derivative of the function and set it equal to #0#:
#dy/dx=xcosx+sinx#
#(d^2y)/(dx^2)=-xsinx+cosx+cosx=-xsinx+2cosx#
#-xsinx+2cosx=0#
#xsinx=2cosx#
#xtanx=2#
#tanx=2/x#
We need to solve for #x# using graphing a utility for this equation. In the graph below, we have the following curves in the interval of #-2pi < x < 2pi# :
#y=xsinx# in red
#y=tanx# in green
#y=2/x# in purple
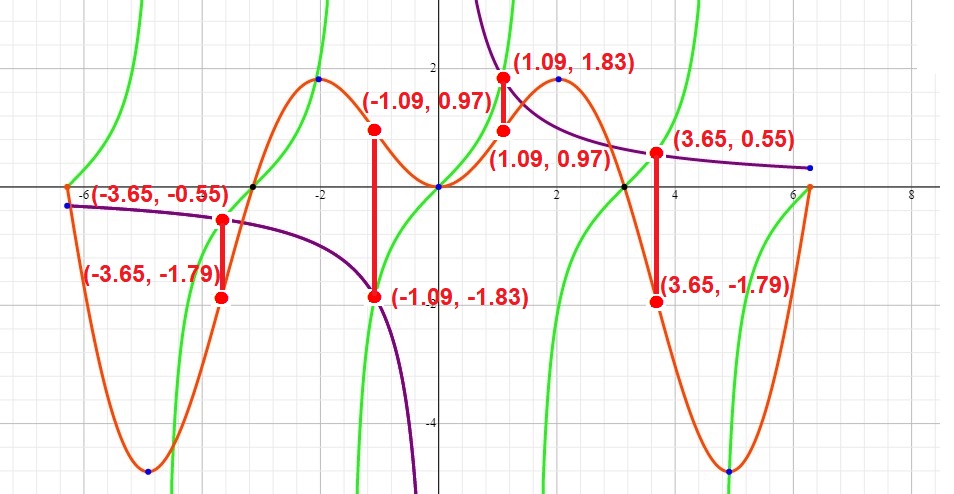
We examine the points of intersection between the green and purple curves and find the four points as follows:
#(-3.65, -0.55), (-1.09, -1.83), (1.09, 1.83), (3.65, 0.55)#
The #x#-coordinates of these points are the #x#-coordinates of points of inflection for #y=xsinx#.
We can plug these into the function #y=xsinx# and calculate the #y#-coordinates of the points of inflection. I have drawn red vertical lines from these four points to #y=xsinx#. As you can see, the coordinates of the inflection points are:
#(-3.65, -1.79), (-1.09, 0.97), (1.09, 0.97), (3.65, -1.79)#
To find the #x# values where #y=xsinx# is concave or convex, you would have to conduct the second derivative test by trying values of #x# to the right and left of each of the four #x values# we obtained from solving the second derivative function. If the result is negative the graph is convex and if positive it is concave.
We can also examine this on the graph visually. The results, in the interval #(-2pi < x < 2pi), #are:
#color(red)("The graph is concave in")#:
#color(red)((-2pi < x < -3.65), (-1.09 < x < 1.09), (3.65 < x < 2pi))#
#color(red)("The graph is convex in")#:
#color(red)((-3.65 < x < -1.09), (1.09 < x < 3.65))#


