Question

The graph of the function f(x)=x^2 - 2x. draw the line tangent to the point (0,0). then estimate the slope at the point?

Answer 1

`m=-2`

Explanation:

.

`y=x^2-2x`

We can find the slope of the tangent to the curve by taking its derivative and evaluating it at the point of tangency:

`dy/dx=2x-2=2(0)-2=0-2=-2`

`m=-2`

We can now write the equation of the tangent line:

`y=mx+b`

`y=-2x+b`

We then use the coordinates of the point of tangency to solve foe `b` which is the `y`-intercept of the line:

`0=-2(0)+b`

`0=0+b`

`b=0`

Therefore, the equation of the tangent line at `(0,0)` is:

`y=-2x`

The graph below shows the function of the parabola in purple and the tangent line in red:

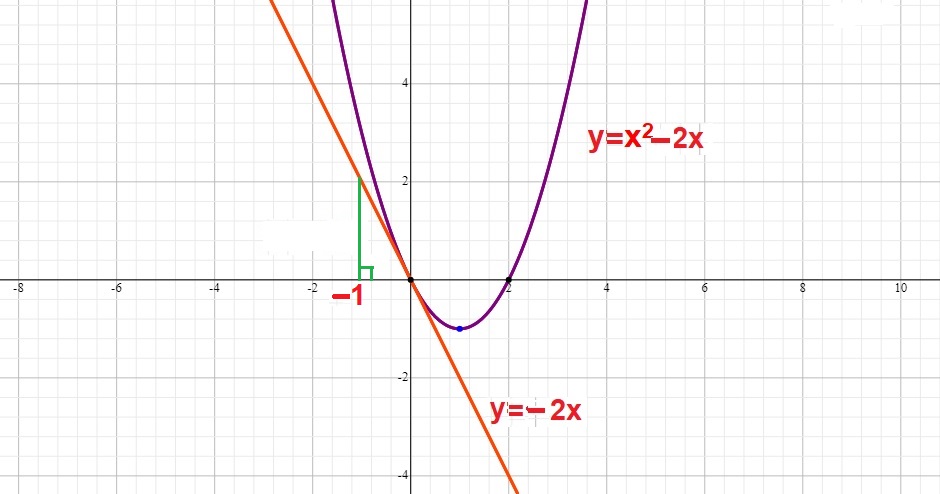
If you wanted to estimate the slope you could visually inspect the graph and see that the slope is:

`("Rise")/("Run")`

Then pick a point on the `x`-axis, `x=-1` and draw a vertical line up to the tangent line. This line is shown in green.

Now, you can estimate the length of the green line which is the `("Rise")`. It appears to be about `2`. The `("Run")` is `-1`. Therefore,

`("Rise")/("Run")=2/(-1)=-2`

If we guess at two values for the `("Rise")`, one slightly larger and one slightly smaller then `2`, such as `2.1` and `1.9` and write the equation of the tangent line with each slope value we will have:

`x=2.1, :. y=-2.1x`

`x=1.9, :. y=-1.9x`

We can test each one by setting the equation of the tangent line equal to the equation of the curve and solving for the `x`-coordinates of the intersection points.

`x^2-2x=-2.1x, :. x^2+0.1x=0, :. x(x+0.1)=0, :. x=0 and -0.1`

Plugging these values into the equation of either function will give us the `y`-coordinates of these points.

`x=0, y=0, and x=-0.1, y=0.2`

This means the line intersects the parabola at two points:

`(0,0) and (-0.1,0.2)`

which means the line is not a tangent line.

Let's test the other value for `("Rise")`:

`x^2-2x=-1.9x, :. x^2-0.1x=0, :. x(x-0.1)=0, :. x=0 and 0.1`

`x=0, y=0, and x=0.1, y=-0.2`

This mean th eline intersects the parabola at two points:

`(0,0) and (0.1,-0.2)`

which again means the line is not a tangent line.

This trial and error process will result in `("Rise")=2`, `m=-2`, and the equation of the tangent line to be:

`y=-2x`