The graph of the function (x^2 + y^2Ž)^2 = 4x^2y is a double folium as shown below. (a) Find, algebraically, all points on the curve with y = 1? (b) Verify that the slopes of tangent lines to both points with y = 1 is equal to 0?

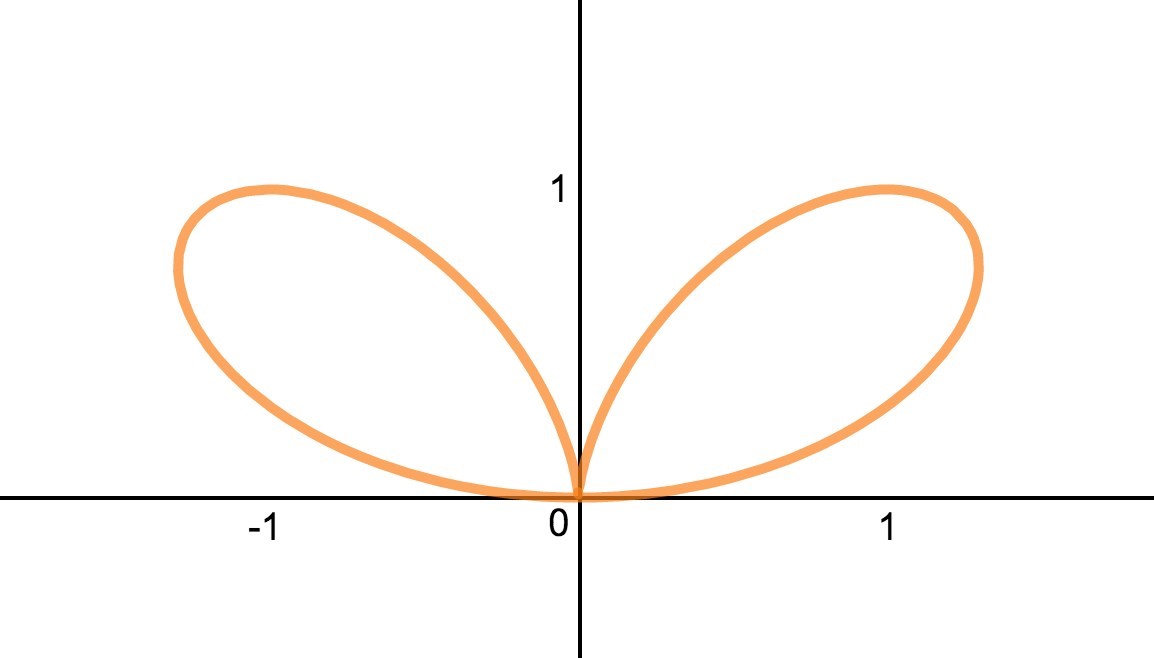
enter image source here

1 Answer
Steve M
Mar 12, 2017

We have:

# (x^2+y^2)^2 = 4x^2y #

Part (A)

# y=1 => (x^2+1)^2 = 4x^2 #

# :. x^4+2x^2+1 = 4x^2 #
# :. x^4-2x^2+1 = 0 #
# :. (x^2-1)^2 = 0 #
# :. x^2-1= 0 #
# :. x^2= 1 #
# :. x \ = +-1 #

So the coordinates are #(1,1)# and #(-1,1)#.

Part (B)
Differentiating implicitly using the chain rule and product rule we get:

# 2(x^2+y^2)(2x+2ydy/dx) = (4x^2)(dy/dx) + (8x)(y) #

We don't need to find an explicit expression for #dy/dx#, just its value when #x=+-1# and #y=1#. Substituting #x^2=1# and #y=1# gives:

# 2(1+1)(2x+2dy/dx) = (4)(dy/dx) + 8x #
# :. 4(2x+2dy/dx) = 4dy/dx + 8x #
# :. 2x+2dy/dx = dy/dx + 2x #
# :. 2dy/dx = dy/dx #
# :. dy/dx = 0 \ \ \ \# QED

Related questions
See all questions in Tangent Line to a Curve
Impact of this question
5700 views around the world
You can reuse this answer
Creative Commons License