Question

The lattice energy of CsI(s) is −604 KJ/mol, and the enthalpy of solution is 33 KJ/mol. How would you calculate the enthalpy of hydration (KJ) of 0.65 moles of CsI? Enter a numeric answer only, do not include units in your answer?

Answer 1

Let's define what we have.

Energy stored within the lattice structure:

`DeltaH_"lattice" = -"604 kJ/mol"`

Enthalpy of the overall solvation of the solid:

`DeltaH_"soln" = "33 kJ/mol"`

Enthalpy of replacing the old interactions with new interactions with water:

`DeltaH_"hydr" = ?`

Since you surround a solid with water to hydrate it, breaking the ion-ion interactions to make ion-dipole interactions, and since within the same context, ion-ion interactions are stronger than ion-dipole interactions, some excess energy is released; thus, enthalpy of hydration should be exothermic.

Breaking a lattice means that you've transferred energy into the lattice to disrupt its interactions and give its gaseous constituent ions, so the enthalpy of the lattice energy must be endothermic.

Note the Born-Haber-like cycle going on here:

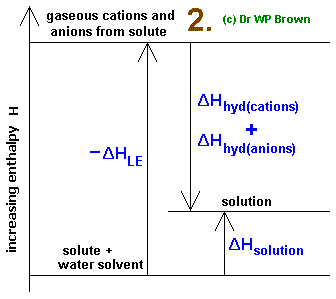
You read this Born-Haber-like cycle diagram by noting that up arrows imply adding, and down arrows imply subtracting.

Thus, it sounds like the following equation makes sense:

`\mathbf(DeltaH_"soln" = (-DeltaH_"hydr") + (-DeltaH_"lattice"))`

As a result, we should get:

`color(green)(DeltaH_"hydr") = - DeltaH_"soln" - DeltaH_"lattice"`

`= - "33 kJ/mol" - ( -"604 kJ/mol")`

`color(green)("= 571 kJ/mol")`

Finally, just multiply by `"0.65 mol"` to ALMOST get your actual answer.

`=> color(green)(" 371.15 kJ")`

And remember that units are already written next to your answer, so you only need the numeric result. Also, like just mentioned, enthalpy of hydration is exothermic.

Although the given answer is positive in sign, remember that we had reversed the sign to line up with the diagram telling us to subtract the enthalpy of hydration, so it's actually supposed to be `color(blue)(-"371.15 kJ")`.