Question

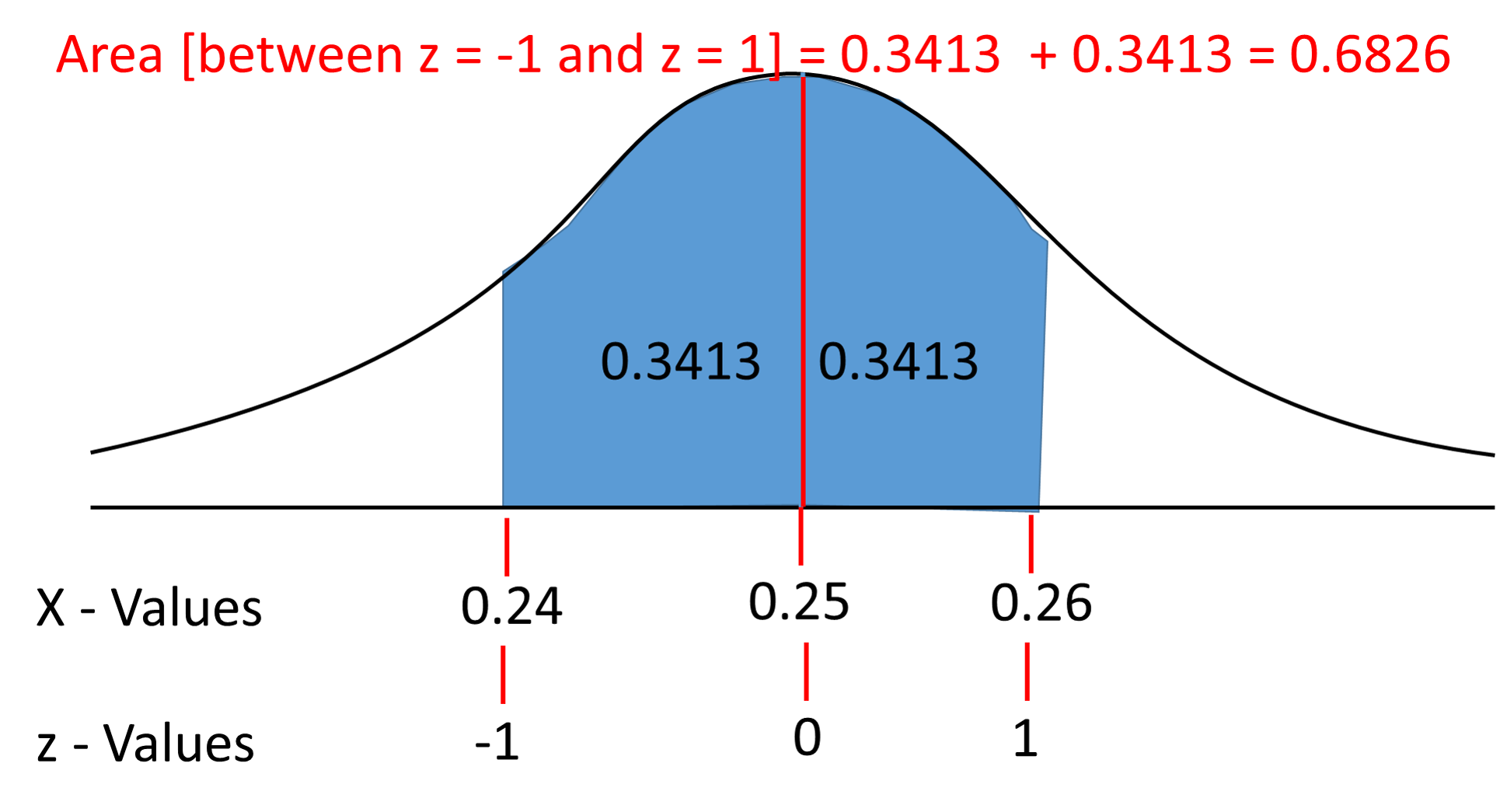
The length of a screw produced by a machine is normally distributed with a mean of 0.25 inches and a standard deviation of 0.01 inches. What percent of screws are between 0.24 and 0.26 inches?

Answer 1

Screws between 0.24 and 0.26 inches = 68.26%

Explanation:

Given -

Mean `barx = 0.25`
SD `sigma=0.01`

Values are normally distributed.

Look at the graph.

Mean is presented exactly at the middle along the X-axis.
The other two `x` values are 0.24 and 0.26

They are also represented along the X - axis.

Their corresponding `z` values are represented below the `x` values, using the formula `z=(x-mu)/sigma`

At `x=0.25; z= (0.25-0.25)/0.01=0/0.01=0`

At `x=0.26; z= (0.26-0.25)/0.01=0.01/0.01=1`

At `x=0.24; z= (0.24-0.25)/0.01=-0.01/0.01=-1`

Using the Area under Normal Distribution Table you have to find the area between `z=0 and z=1`

This is same for `z=0 and z=-1`

Area between `[z=-1 and z=1] =` area between `[z=0 and z=-1] +` area between`[z=0 and z=1]`

Area between `[z=-1 and z=1] = 0.3413 + 0.3413=0.6826`

If one screw is taken at random the probability of its length fall between 0.24 and 0.26 inches is `=0.6826`

Then percentage of screws fall between 0.24 and 0.26 inches is `=0.6826 xx 100=68.26`

Normal Distribution Part - 1

Normal Distribution Part - 2