The length of each side of an equilateral triangle is increased by 5 inches, so, the perimeter is now 60 inches. How do you write and solve an equation to find the original length of each side of the equilateral triangle?
1 Answer
Nov 11, 2016
I found:
Explanation:
Let us call the original lengths
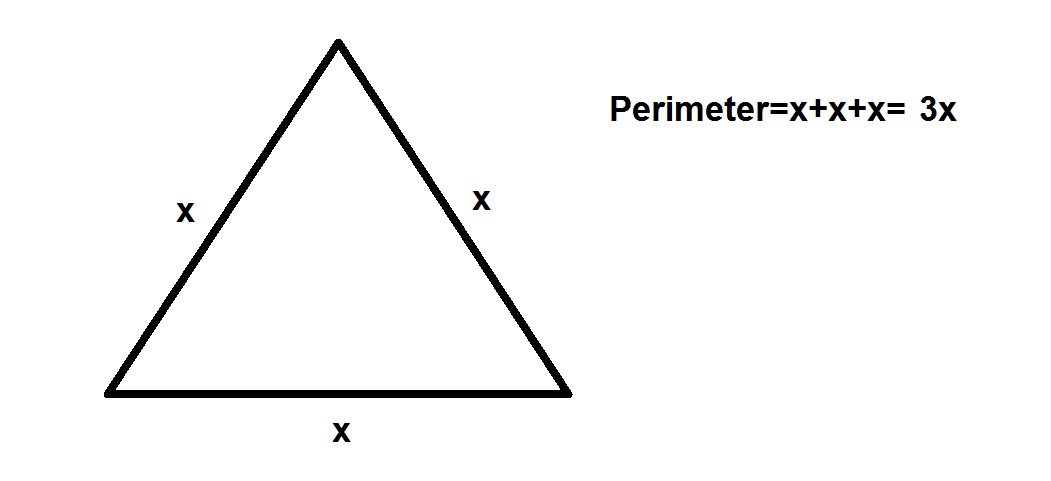
Increasing of
rearranging:

