The length of the shadow of a pillar is increased by #60m# when the angle of elevation of the sun becomes #30^@# from #45^@#. Find the height of the pillar ?

The length of the shadow of a pillar is increased by #60m# when the angle of elevation of the sun becomes #30^@# from #45^@#. Find the height of the pillar ?

1 Answer
IZUkuABA
Jun 25, 2018

height=81.967 metre(approx.)

Explanation:

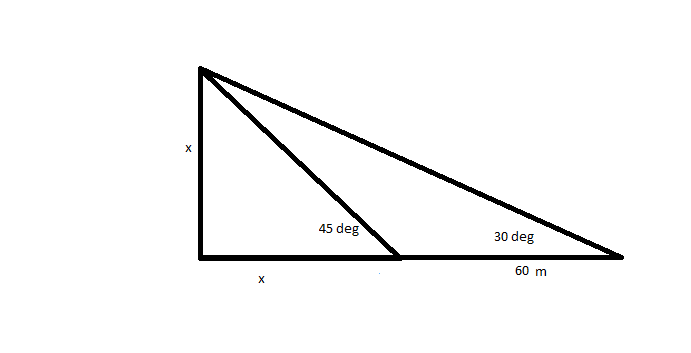
enter image source here

we have # tan 45= x/x#
and # tan 30=x/x+60#
#=> 1/sqrt3=x/x+60#................tan30=#1/sqrt3#
#=>x+60=sqrt3*x#
#x(sqrt3-1)=60; => x(0.732)=60 ;=> x~81.967 m#
hence height =81.967 metre

Related questions
Impact of this question
1198 views around the world
You can reuse this answer
Creative Commons License