The lengths of a certain species of fish were found to be normally distributed. The mean length is 93 cm with a standard deviation of 12 cm. In a school of 360 of these fish, about how many would be longer than 81 cm?
1 Answer
Apr 21, 2017
Number of fish having a length greater than 81 cm out of 360
Explanation:
Given -
Mean length of fish
SD
Number of fish having a length greater than 81 cm out of 360.
Find the value of
#z=(x-barx)/sigma=(81-93)/12=(-12)/12=-1#
Find the Area between
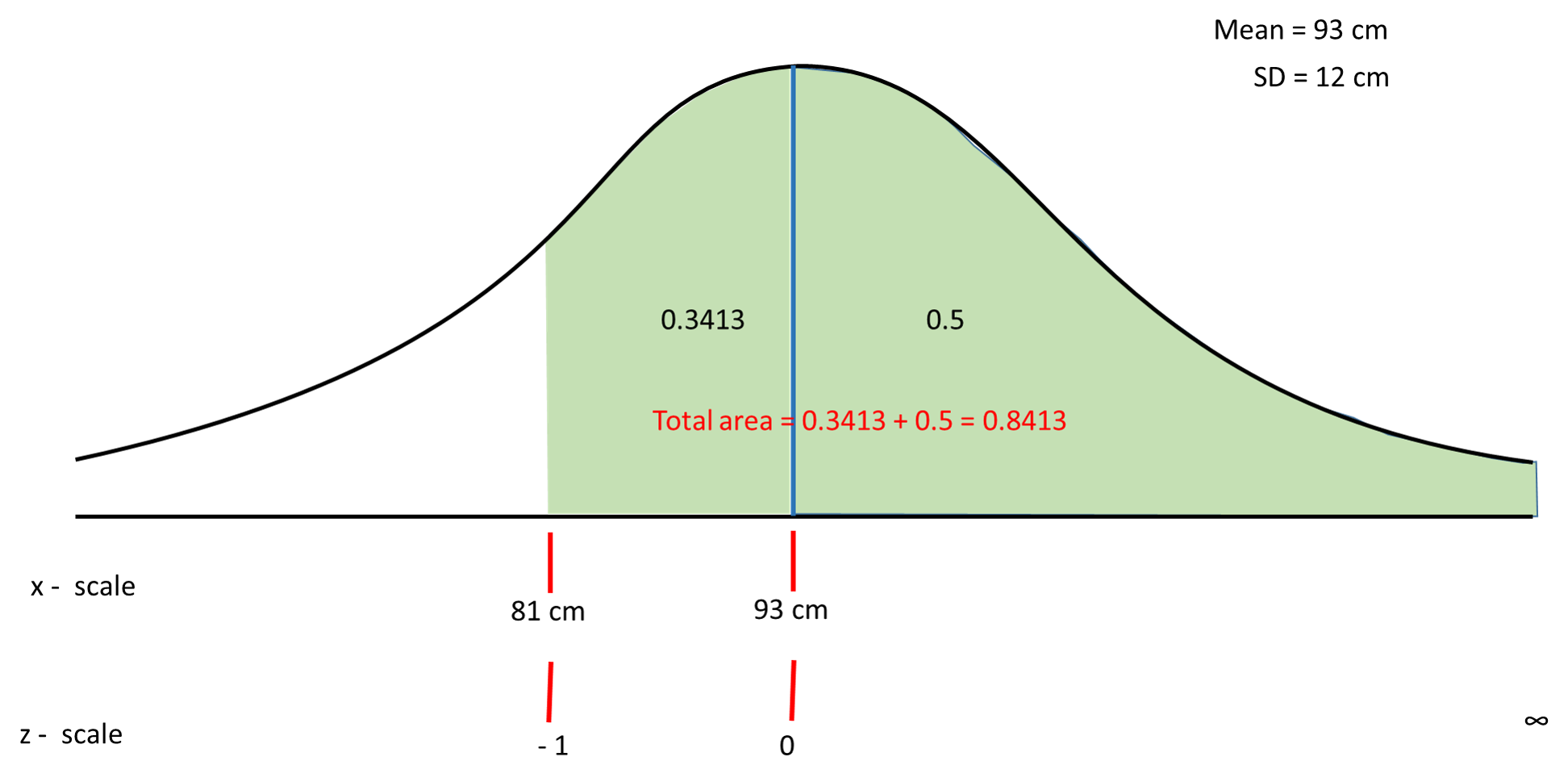
Area between
Area between[
Number of fish having a length greater than 81 cm out of 360

