The particle p is released from rest at the top of a smooth plane inclined at angle a where sina=16/65.the distance travelled by P from top to bottom is S metres and speed of P at bottom is 8ms^-1 find S and hence speed of P when it has travelled 1/2S?
2 Answers
Explanation:
Draw a diagram!!!!
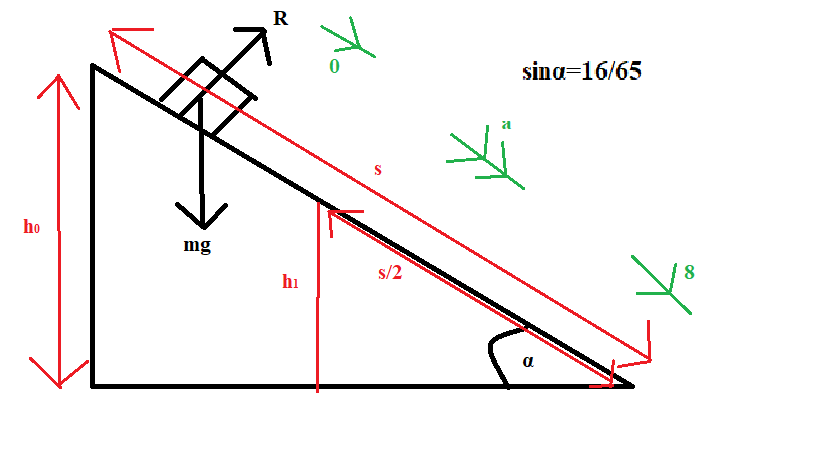
I've drawn the only forces acting on P; its weight (
As a reminder,
To first find GPE, we need h (marked on my diagram as
Yes, m is an unknown, so we need to get rid of it at some point.
by conservation of energy:
Taking
We can do the same thing with
We don't know m or v; this is as simple as we can go right now.
By conservation of energy
Alternate solution.
Explanation:
Particle p of mass
#vecF=mveca#
Acceleration in the downwards direction is equal to
#a=(mgsina)/m#
#=>a=gsina#
#=>a=9.81xx16/65 \ms^-2#
Distance
#v^2-u^2=2as#
Inserting given values we get
#8^2-0^2=2(9.81xx16/65)S#
#=>S=64/(2(9.81xx16/65))#
#=>S=13.25\ m#
Using same kinematic expression to find velocity when particle traveled a distance of
#(v_(S/2))^2+0^2=2(9.81xx16/65)8/2#
#=>v_(S/2)=sqrt(8(9.81xx16/65))#
#=>v_(S/2)=4.4\ ms^-1#
