The path of a football kicked by a field goal kicker can be modeled by the equation # y = -0.04x^2 + 1.56x#, where x is the horizontal distance in yards and y is the corresponding height in yards. What is the approximate maximum height of the football?
1 Answer
Explanation:
We are essentially be asked to find the vertex which is the maximum height of the football.
The formula for finding the vertex is
From the given equation,
When we substitute this into the formula:
What we just found is actually the
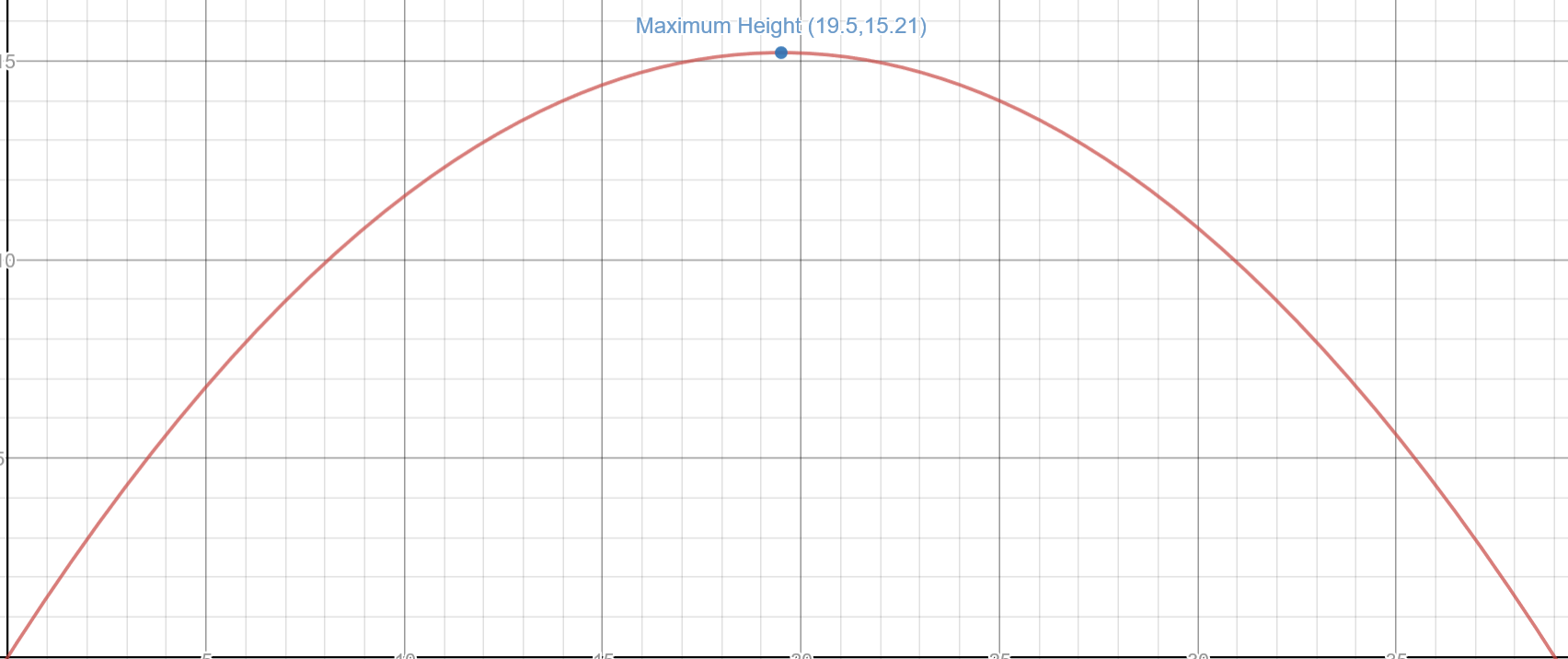
From all this information we can conclude that: When the ball travels a horizontal distance of 19.5 yards, the ball will reach its maximum height of 15.21 yards
P.S, It's always good to visualize the problem. Below is what the path of the ball looked like based on the function given in the problem. You can also see where the maximum height occurred which correctly mirrors our results: