The perimeter of a rectangle is represented by 8y meters and the area is (6y+3) square meters. a) write two equations in terms of x and y for the perimeter and the area b) determine the perimeter and the area ?

Question

3135 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-04-06T11:16:32

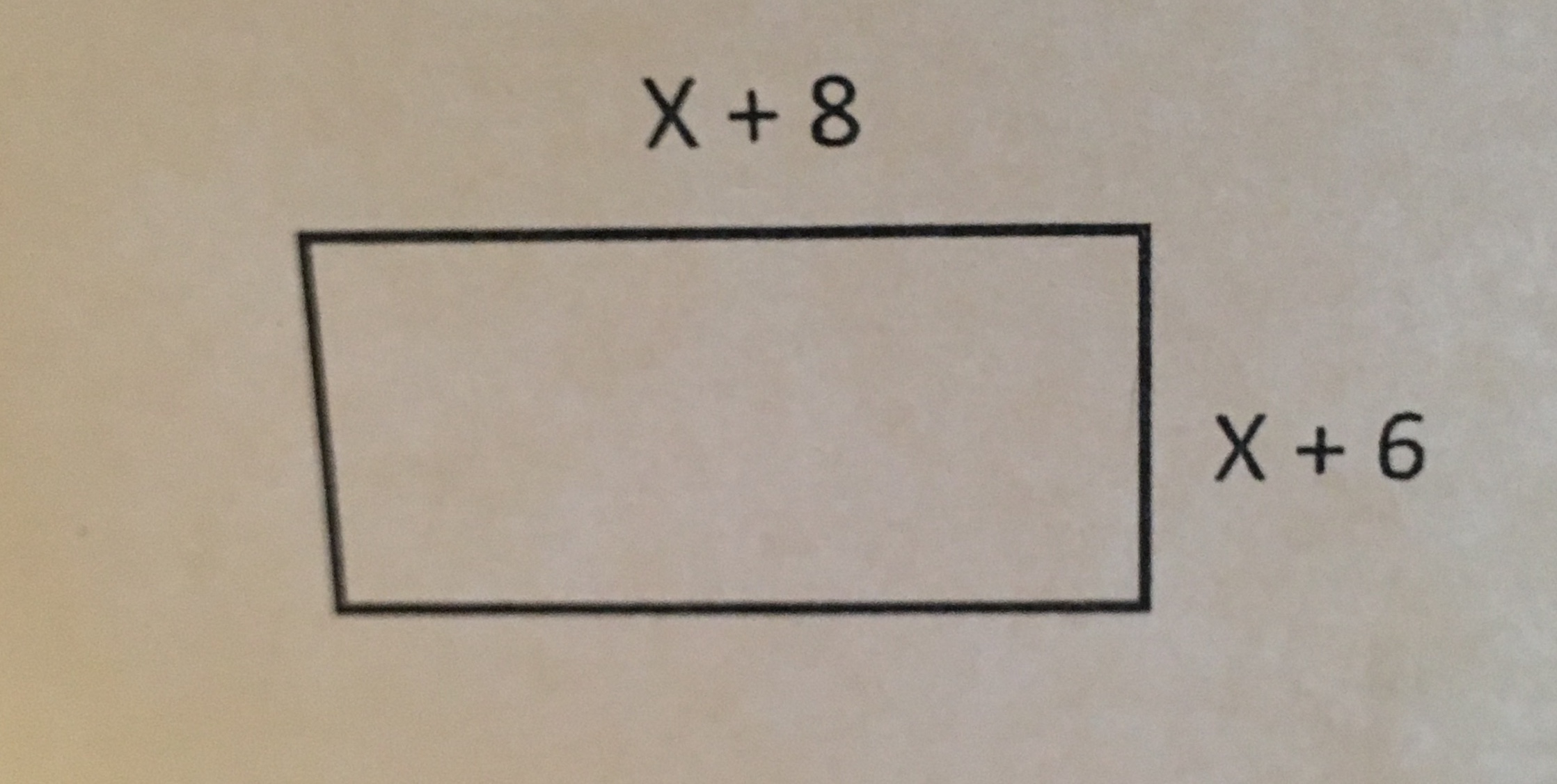
Given length of th rectangle # l=x+8#

width of th rectangle # w=x+6#

Its perimeter becomes #2(l+w)=8y#

#2(x+8+x+6)=8y#

#=>4(x+7)=8y#

#=>x=2y-7..........[1]#

Again area of the rectangle #lxxw=6y+3#

#(x+8)(x+6)=6y+3......[2]#

From [1] and [2] we get

#(2y-7+8)(2y-7+6)=6y+3#

#=>(2y+1)(2y-1)=6y+3#

#=>4y^2-6y-4=0#

#=>2y^2-3y-2=0#

#=>2y^2-4y+y-2=0#

#=>2y(y-2)+1(y-2)=0#

#=>(2y+1)(y-2)=0#

#8y# being the perimeter #y<0# is rejected

So #y=2#

So perimeter #=8y=8xx2=16# m

And area #=6y+3=6xx2+3=15m^2#