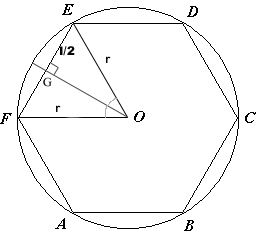
The perimeter of a regular hexagon is 48 inches. What is the number of square inches in the positive difference between the areas of the circumscribed and the inscribed circles of the hexagon? Express your answer in terms of pi.
1 Answer
Explanation:
Perimeter of regular hexagon
Side of hexagon
Regular hexagon consists of 6 equilateral triangles of side a each.
 )
)
Inscribed circle : Radius