Question

The perimeter of a regular nonagon is 72 meters. Find the area of the polygon in square meters?

The image description of the nonagon is shown below, drawn with a TI-nspire graphing calculator.

Answer 1

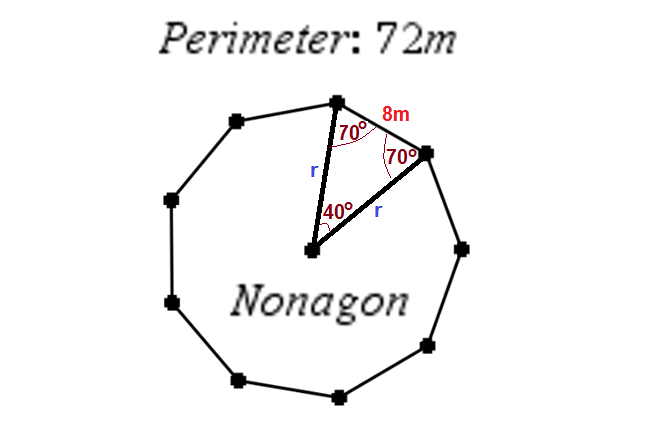
Given that perimeter of the regular nonagon `P=72m`

The each side of the regular nonagon will be `a=P/9=72/9=8m`

Each side will form an isosceles triangle if its end points are joined with the center of the circumscribing circle as shown in figure. Let the radius of circumscribing circle be `r`m. The vertical angle of each isosceles triangle will be `theta=360^@/9=40^@`. Hence each of other two angles will be `=(180-40)/2=70^@`

Now by sine law we have

`r/(sin70^@) = a/sin40^@`

`=>r=sin70^@/(sin40^@)xx8m`

So area of each isosceles triangle `Delta=1/2r^2sin40^@`

Hence area of nonagon

`"Area"=9Delta=9/2r^2sin40^@`

`=9/2xx(sin^2 70^@)/sin^2 40^@xx64xxsin40^@`

`=9xx32xx(sin^2 70^@)/(sin 40^@)=395.6m^2`