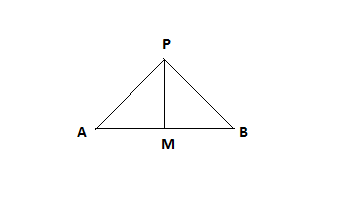
Given AP = BP and AM = BM To prove hat (AMP) = hat (BMP) = 90^@
"In triangle APB", AP = BP," hence it's an isosceles triangle"
:. hat (PAM) = hat (PBM)
"Since " AM = BM, hat (APM) = hat (BPM), " Equal sides will have equal angle opposite to them theorem"
"We know sum of three angles of a triangle equals " pi^c or 180^@
"Hence, in triangle APM ", pi - (hat (PAM) + hat (APM)) = hat (PMA)
"Similarly in triangle BPM", pi - (hat (PBM) + hat (BPM)) = hat (PMB)
"Since " hat (PAM) + hat (APM) = hat (PBM) + hat (BPM), hat(AMP) = hat (BMP)
But hat (AMP), hat (BMP) " are supplementary angles"
"i.e. " hat (AMP) + hat (BMP) = pi^c " or " 180 ^@
:. hat (AMP) = hat (BMP) = pi/2 " or " 90^@
"That means "bar(PM) " is the perpendicular bisector of "bar(AB)

