The question is below?

A square based pyramid is on the top of cuboid having length and breadth equal to 6 cm and height equal to 10 cm. If the TSA of the combined solid object is #336 cm^2# then find the height of the pyramid.

1 Answer
P dilip_k
Jun 7, 2018

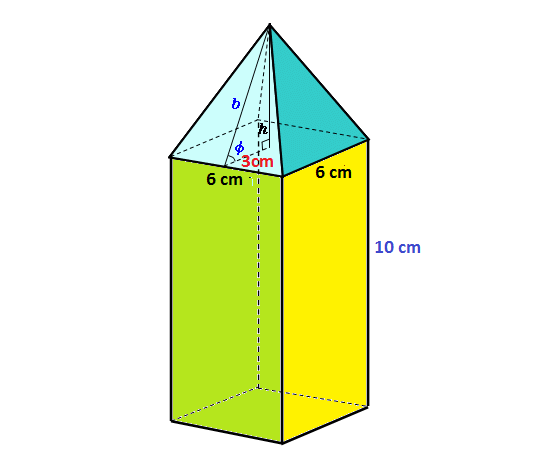drawn

Here the base of the pyramid must be #6xx6cm^2# square.

If the height of the pyramid be #h# cm,then the height of each triangular side of the pyramid will be #b=sqrt(h^2+3^2)#cm. Base of each triangular face being #6# cm the total surface area of 4 triangular face will be #=4*1/2*6*sqrt(h^2+3^2)#

#=12sqrt(h^2+3^2)cm^2#

So total area of other 5surfaces will be #=(4*6*10+6^2)=276cm^2#

Hence by the problem

#12sqrt(h^2+3^2)+276=336#

#=>12sqrt(h^2+3^2)=60#

#=>sqrt(h^2+3^2)=5#

#=>h^2+9=25#

#=>h=sqrt16 =4# cm

Related questions
Impact of this question
1089 views around the world
You can reuse this answer
Creative Commons License