The question is below?
If #I_n# be the area of n-sided regular polygon inscribed in a circle of unit radius and #O_n# be the area of the regular polygon circumscribing the given circle prove that
#I_n=((O_n)/2)[1+sqrt(1-((2I_n)/n)^2)]#
If
1 Answer
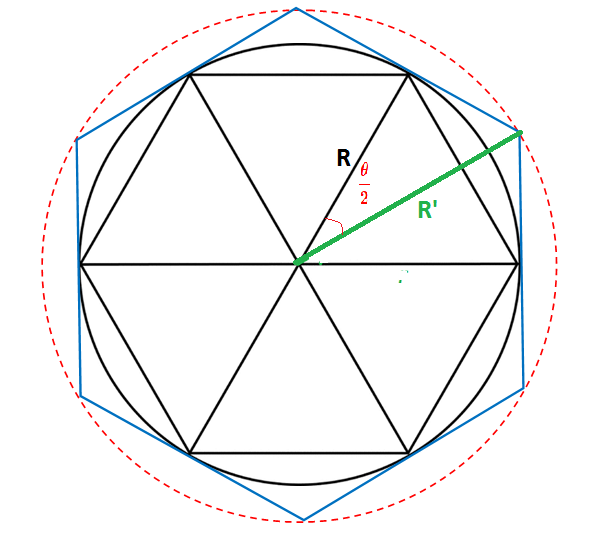
Given that an n-sided regular polygon is inscribed in a circle of unit radius i.e.
Let
Now area of the inner smaller polygon will be
So
Now
Again the area of the larger outer polygon will be
So

