The radii of two concentric circles are 16 cm and 10 cm. #AB# is a diameter of the bigger circle. #BD# is tangent to the smaller circle touching it at #D#. What is the length of #AD#?
2 Answers
Explanation:
Adopting the origin
here
Solving for
Subtracting the first from the second equation
Finally the sought distance is
or
Explanation:
If
The point
There are many ways to do that. An alternative method is
then

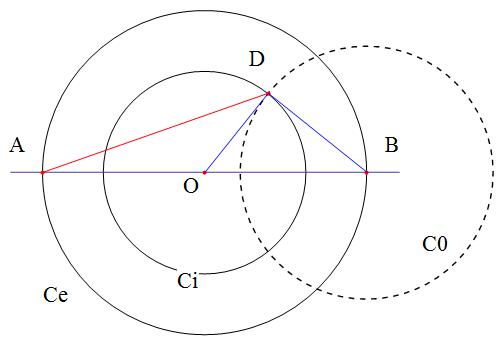
As per given data the above figure is drawn.
O is the common center of two concentric circles
Let
In
Applying cosine law in


