Question

The resultant of two vectors P and Q is R.If Q is doubled then the new resultant vector is perpendicular to P.Then R is equal to?

Answer 1

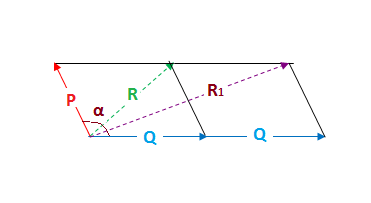
Let the angle between two vectors `P and Q` be `alpha` and their resultant is `R`

So we can write

`R^2=P^2+Q^2+2PQcosalpha......[1]`

When Q is doubled then let the resultant vector be `R_1`, So we can write

`R_1^2=P^2+4Q^2+4PQcosalpha......[2]`

Again by the given condition `R_1` is perpendicular to `P`

So `4Q^2=P^2+R_1^2......[3]`

Combining [2] and [3] we get

`R_1^2=P^2+P^2+R_1^2+4PQcosalpha`

`=>2PQcosalpha=-P^2......[4]`

combining [1] and [4] we get

`R^2=P^2+Q^2-P^2`

`=>R=Q`