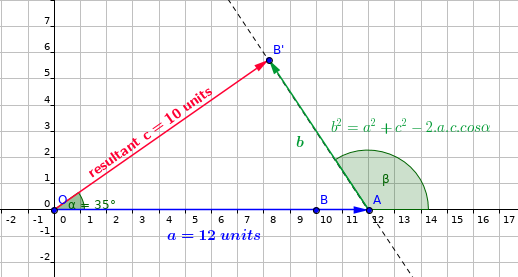
#"resultant c=10 units"#
#"first component a=12 units"#
#"second component b=?"#
#"angle between a and c "alpha=35 " deg"#
#"the triangle method is used in the drawing."#
#vec c=vec a+vec b#
#b^2=a^2+c^2-2*a*c*cos 35#
#cos 35=0.81915204#
#b^2=12^2+10^2-2*12*10*0.81915204#
#b^2=144+100-240*0.81915204#
#b^2=244-196.596#
#b^2=47.404#
#sqrt(b^2)=sqrt(47.404)#
#b=6.89" units"#
#"angle between two components(a,b):"#
#c^2=a^2+b^2+2*a*b*cos beta#
#cos beta=(c^2-(a^2+b^2))/(2*a*b)#
#cos beta=(100-(144+47.404))/(2*12*6.89)#
#cos beta=(100-191.404)/(165.36)#
#cos beta=(-91.404)/(165.36)#
#cos beta=-0.55275762#
#beta=123.56" deg"#


