Question

The solid whose base is the region bounded by y= x^2 and the line y=1 and whose cross sections perpendicular to the base and parallel to the x-axis are squares? .

Answer 1

`A_("Solid")=2`

Explanation:

.

`y=x^2` is a parabola (shown in purple) opening up with its vertex on the origin.

`y=1` is a horizontal line (shown in red). The region bound by these two curves is shaded in yellow:

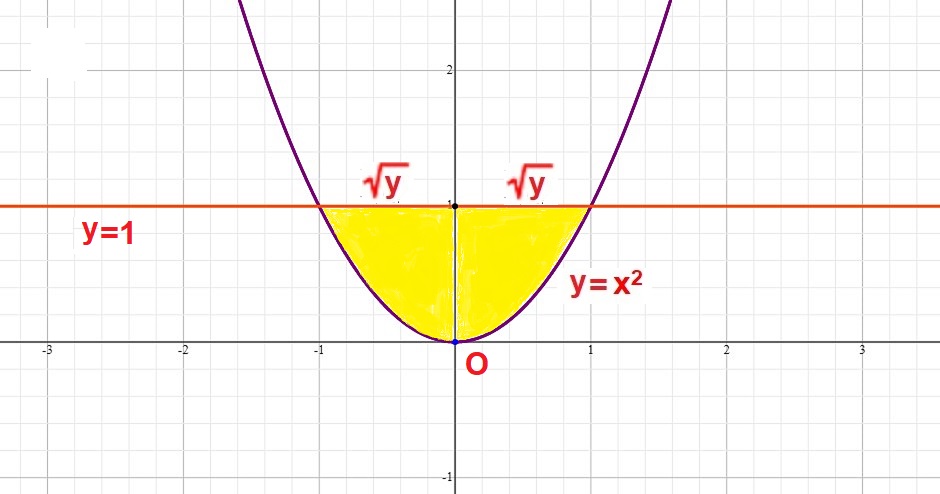
The solid described in the problem is based on this yellow region with thin square plates perpendicular to the yellow base and parallel to the `x`-axis.

Let's look at the figure below to get a better idea of the solid described in this problem:

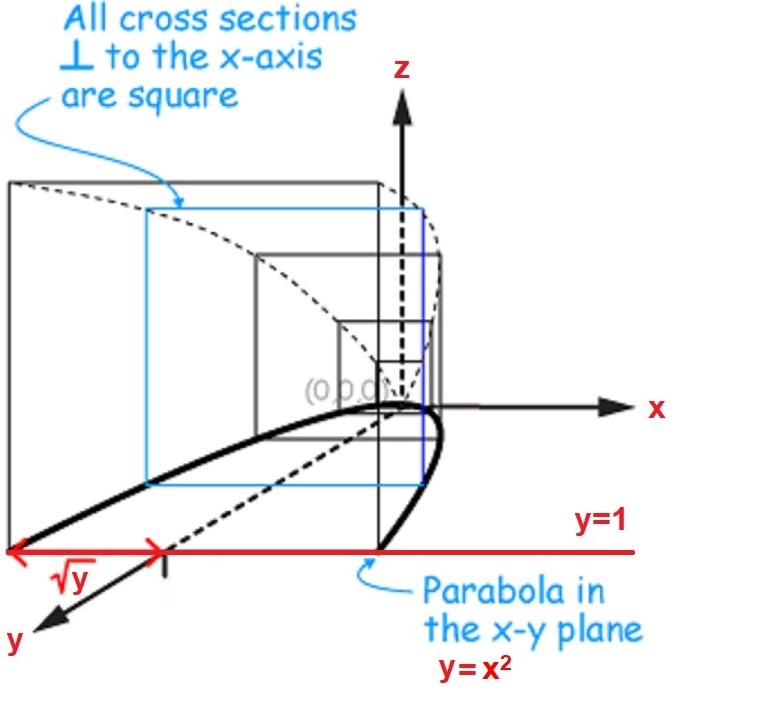
The solid described has a base bounded by the following three curves:

`y=x^2` which is the parabola shown in black.

`y=1` which is the red line parallel to the `x`-axis

`y=0` which is the `x`-axis.

and has a height that is formed by the top sides of all the squares that are parallel to the `x`-axis and perpendicular to the `y`-axis.

These squares have areas that vary from `0` at the origin to `4` at `y=1`. You can see how we arrived at this below:

`x=+-sqrty=+-1`

`a=2(1)=2`

`A_("Square")=a^2=(2)^2=4`

We need to find the volume of this solid. If we imagine two of these squares extremely close together, with the distance between them `=dy`, we can calculate the volume of that slice by multiplying the area of the square by `dy`.

Then we can integrate that function along the `y`-axis between `0` and `1` to get the volume of the solid. This is because the integral adds an infinite number of these volumes together to get the full volume between the `x`-axis and the line `y=1`.

`A_("Square")=(2sqrty)^2=4y`

`A_("Solid")=int_0^(1)4ydy=4int_0^1ydy=4(1/2y^2)=2y^2)_0^1=2`