The successive ionization energies of an element A are as follows?
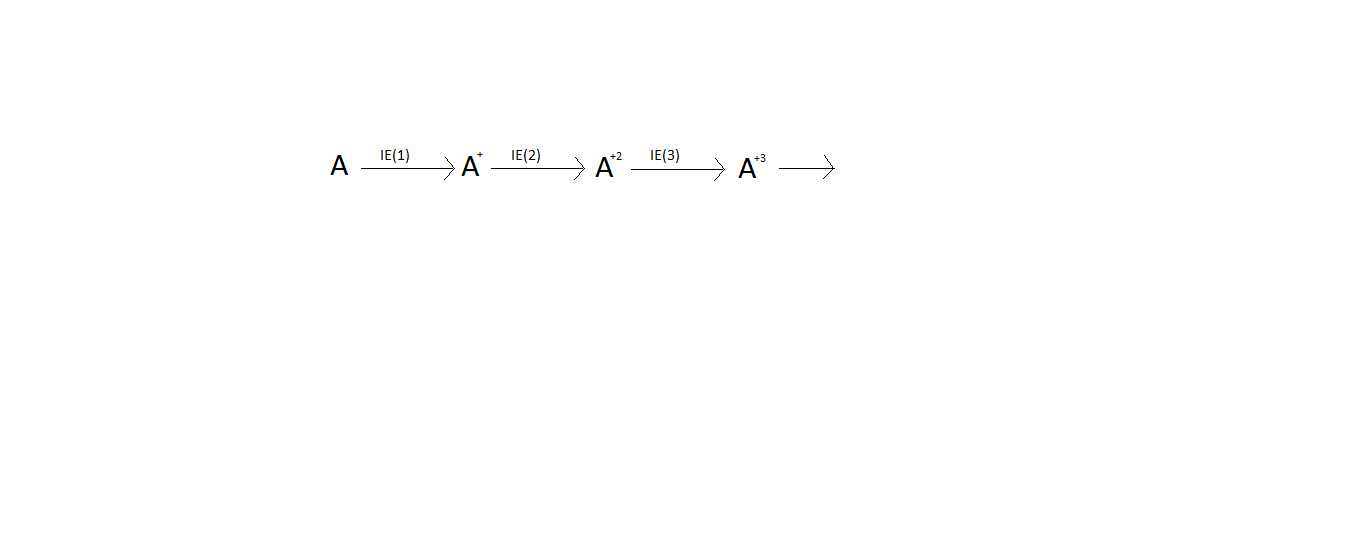
If the IE(1) and IE(3) values are #(27\text{KJ})/\text{mole}# and #(51\text{KJ})/\text{mole}# respectively , then the value of IE(2) is in #(\text{KJ})/\text{mole}# ?
A) #21#
B)#33#
C)#59#
D)#63#
If the IE(1) and IE(3) values are
A)
B)
C)
D)
2 Answers
Would we not expect it to be
Explanation:
On the basis of simple electrostatics (forgot for the moment about energy levels), would we not expect the SECOND oxidation of an element to be GREATER than the first, and LESS than the THIRD...?
And likewise...
And as chemists, as physical scientists, we are obliged to consider the data... Consider successive ionizations represented by the graph...
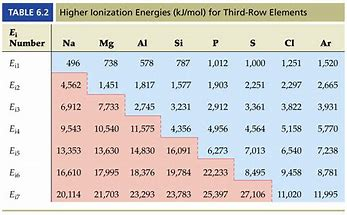
Do these data support or detract from our argument?
OPTION B
Explanation:
clearly the energy required to knock out second electron will be less than the energy required to knock out the third electron(due to increasing effective nuclear charge with each electron gone) .
Hence
And similarly more energy is required to knock out the second electron than the energy required to knock out the outermost valence electron.
Hence
The only option which matches both the criteria is Option B
**


