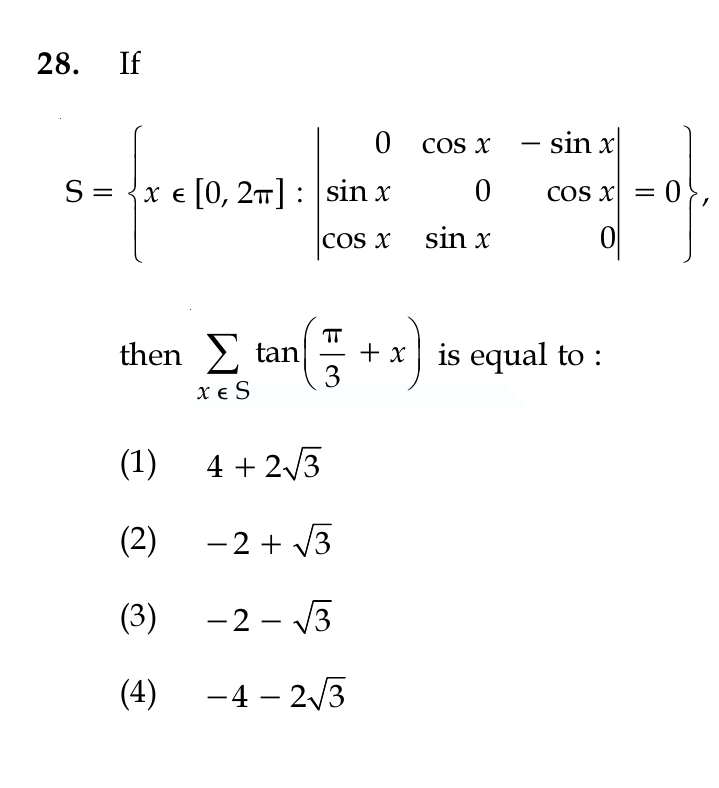|(0,cosx,-sinx),(sinx,0,cosx),(cosx,sinx,0)|=0.
Expanding by the first raw, we have,
:. 0-cosx(0-cos^2x)-sinx(sin^2x-0)=0.
:. cos^3x-sin^3x=0, or, sin^3x=cos^3x......(star).
We must have cos^3x!=0, because," otherwise "cosx=0, and, then,
(star) rArr sin^3x=cos^3x=0," so that, "sinx=0.
rArr cos^2x+sin^2x=0+0=0, a contradiction.
So, dividing (star)" by "cos^3x!=0, "we get, "tan^3x=1.
:. tanx=1, &, x in [0,2pi], x=pi/4,or, x=pi/4+pi=5/4pi.
:. S={pi/4,5pi/4} rArr AA x in S, tanx=1.
:. sum_( x in S)tan(pi/3+x),
=tan(pi/3+pi/4)+tan(pi/3+5pi/4),
={tan(pi/3)+tan(pi/4)}/{1-tan(pi/3)tan(pi/4)}
+{tan(pi/3)+tan(5pi/4)}/{1-tan(pi/3)tan(5pi/4)},
=(sqrt3+1)/(1-sqrt3)+(sqrt3+1)/(1-sqrt3),
={2(sqrt3+1)}/(1-sqrt3)xx(1+sqrt3)/(1+sqrt3),
=2/{1-3)(1+sqrt3)^2.
rArr sum_( x in S)tan(pi/3+x)=-(1+2sqrt3+3),
showing that the right option is (4): -4-2sqrt3.
Feel & Spread the Joy of Maths.!