The volume of ice-cream in the cone is half the volume of the cone. The cone has a 3cm radius and 6cm height. What is the depth of the ice cream, correct to two decimal places?

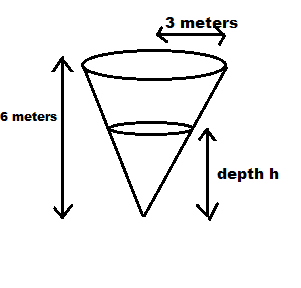
enter image source here
-measurements is in cm

1 Answer
Sean
Jan 28, 2018

#h=4.76# #cm#

Explanation:

.

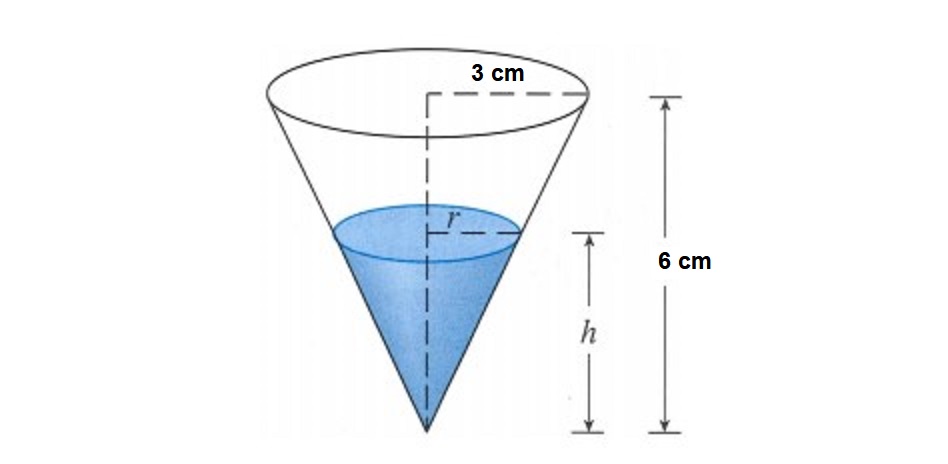
enter image source here

#V_"Cone"=piR^2H/3#

#R=3# #cm#

#H=6#

#V_"Cone"=pi(3)^2(6/3)=18pi# #cm^3#

#V_"Ice Cream"=(18pi)/2=9pi# #cm^3#

#r# is the radius of the Ice Cream.

#h# is the height (depth) of the Ice Cream.

The right triangles formed by the height of the cone and the two radii #R# and #r# are similar triangles by #"AA"# theorem. Therefore, the ratio of their corresponding sides are the same:

#h/6=r/3#

#6r=3h#

#r=(3h)/6=h/2#

#V_"Ice Cream"=pir^2h/3#

#V_"Ice Cream"=pi(h/2)^2(h/3)#

#9pi=h^3/12pi#

#9=h^3/12#

#h^3=108#

#h=root(3)108=4.76# #cm#

Related questions
Impact of this question
19421 views around the world
You can reuse this answer
Creative Commons License