Three rods each of mass M and length L, are joined together to form an equilateral triangle. What is the moment of inertia of a system about an Axis passing through its centre of mass and perpendicular to the plane of the triangle?
2 Answers
Explanation:
The moment of inertia of a single rod about an axis passing through its center and perpendicular to it is
That of each side of the equilateral triangle about an axis passing through the triangle's center and perpendicular to its plane is
(by the parallel axis theorem).
The moment of inertia of the triangle about this axis is then
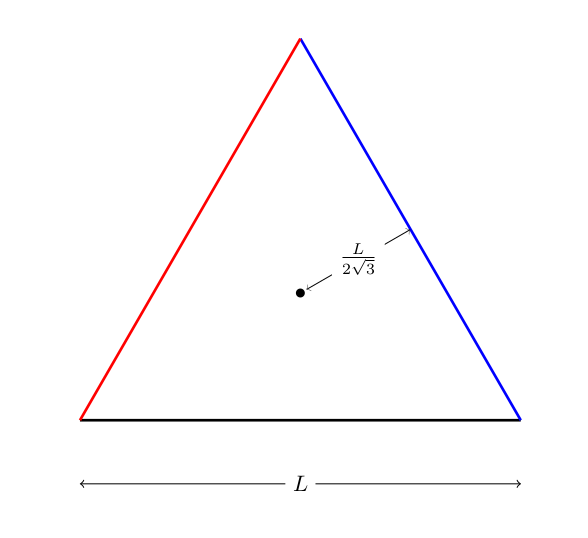
Assuming rods to be thin, position of center of mass of each rod is at the center of rod. As the rods form an equilateral triangle, the center of mass of of the system will be at the centroid of the triangle.
Let
#d/(L/2)=tan30#
#=>d=L/2tan30#
#=>d=L/(2sqrt3)# .....(1)
Moment of inertia of a single rod about an axis passing through the centroid perpendicular to the plane of the triangle using parallel axis therorm is
#I_"rod"=I_"cm"+Md^2#
There are three similarly placed rods, therefore total moment of inertia of three rods would be
#I_"system"=3(I_"cm"+Md^2)#
#=>I_"system"=3I_"cm"+3Md^2# .......(2)
Second term using (1) is
#3Md^2=3M(L/(2sqrt3))^2#
#=>3Md^2=1/4ML^2 # .....(3)
As moment of inertia of one rod about its center of mass is
#I_"cm"=1/12ML^2#
First term in (2) becomes
#3I_"cm"=3xx1/12ML^2=1/4ML^2# ....(4)
Using (3) and (4), equation (2) becomes
#I_"system"=1/4ML^2+1/4ML^2=1/2ML^2\ kgm^2#

