Question

Three vertices of a rectangle have coordinates (3,4), (5-4), and (-7-7) What is the `y` coordinate of the fourth vertex?

Answer 1

`" "`
`color(blue)("y-coordinate value of the fourth vertex [ D ] = 1"`

Explanation:

`" "`
`color(green)("Step 1 :"`

Plot the given points in sequence with Vertex A, Vertex B and Vertex C respectively.

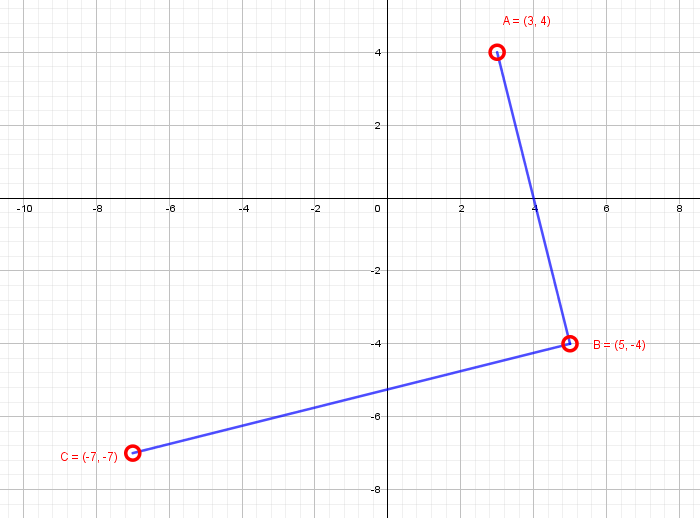
Joint the points `A, B and C` with line segments `AB and BC` as shown.

`color(green)("Step 2 :"`

Use the distance formula to find the magnitudes of the line segments `AB and BC`.

This process explains how it is done using Algebra:

Distance Formula:

`color(blue)(d=sqrt[(x_2-x_1)^2 + (y_2-y_1)^2]`

(a) Distance between the points : `A(3,4) and B(5,-4)`

`x_1=3, y_1=4, x_2=5 and y_2=-4`

`d=sqrt[(5-3)^2+{(-4)-4}^2`

`d=sqrt(2^2+(-8)^2`

`d=sqrt(68)`

`d~~ 8.246211251`

`d=8.25` (2 decimal places)

Hence, the line segment `AB = 8.25` units.

(b) Distance between the points : `B(5,-4 ) and c(-7,-7 )`

`x_1=5, y_1=-4, x_2=-7 and y_2=-7`

`d=sqrt[{(-7)-5}^2+{(-7)-(-4)}^2`

`d=sqrt(144+(-3)^2`

`d=sqrt(144+9) = sqrt(153)~~12.36931688`

`d=12.37` (2 decimal places)

Hence, the line segment `BC = 12.37` units.

`color(green)("Step 3 :"`

Verify these results with geometrical constructions:

(a) Draw a parallel line through the point `A`, with the line parallel to `BC`

(b) Draw a parallel line through the point `C`, with the line parallel to `AB`

(c) `D` is the point of intersection of lines.

(d) Connect points `A and D` and the points `C and D`.

We have a parallelogram.

Measure the lengths of the line segments `AB, BC, CD and AD`.

We find that `AB=8.25, BC=12.37, CD=8.25, AD=12.37`

`AB||CD` and they are also congruent.

`AD||BC` and they are also congruent.

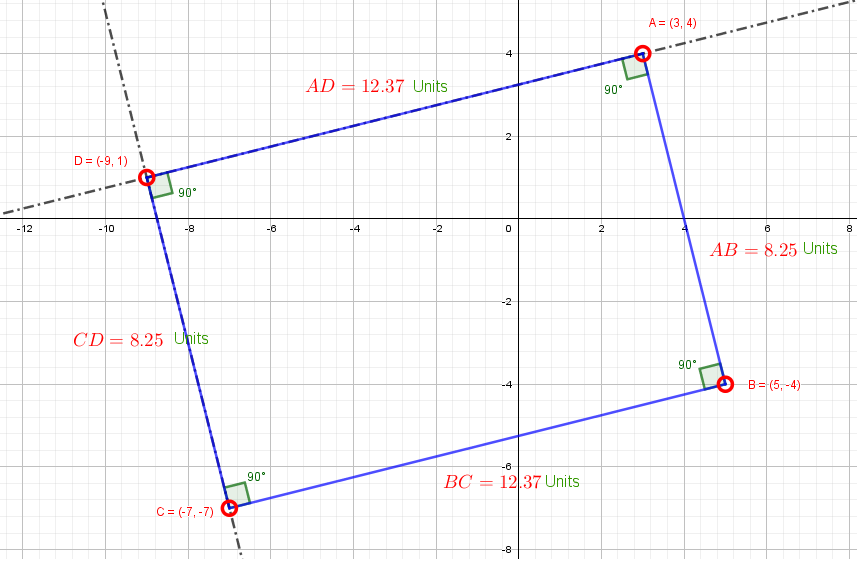
We have two pairs of opposite sides that are parallel and equal.

There are 4 right angles.

Hence, `ABCD` is a rectangle.

Vertex of D to be `(-9, 1)`

Hence the y-coordinate of the Vertex D is `1`.