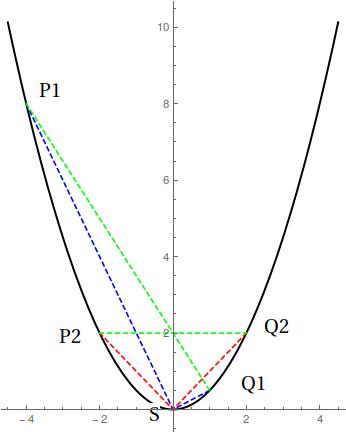
Through the vertex S of a parabola the chord SP and SQ are drawn at right angles.Show that the straight line PQ intersects the axis at a fixed point?

Question

850 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-03-10T16:55:59

See below.

Calling

#S = (0,y_s)#
#P=(x_p,y_p)#
#Q=(x_q,y_q)#
#p = (x,y)#

we have

#y_p = y_s+a x_p^2#
#y_q = y_s+a x_q^2#

Also

#norm(P-Q)^2 = norm(P-S)^2+norm(Q-S)^2# (right angles)

Developing and substituting dependencies we get

#x_px_q(1+a^2x_px_q)=0# or

#x_px_q = -1/a^2#

Now solving the intersection of lines

#L_1->p = P+lambda(Q-P)#
#L_2->p = (0,mu)#

we get

#lambda = x_p/(x_p-x_q)#
#mu = (x_py_q-x_qy_q)/(x_p-x_q)#

and after substituting de dependencies

#y_p = y_s+a x_p^2#
#y_q = y_2+a x_q^2#

we get

#mu = y_s-a x_p x_q#

but

#x_px_q = -1/a^2# hence

#mu = y_s+1/a = C^(te)# which is the vertical intersection coordinate of a generic line #L_1# with the vertical axis

Attached a plot showing the setup for

#a = 0.5#

enter image source here