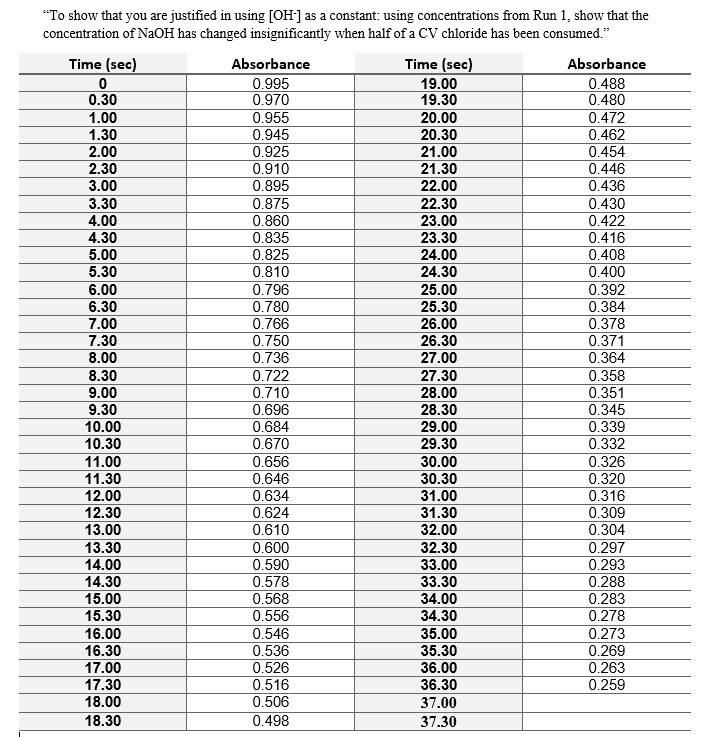
To show that you are justified in using [OH-] as a constant: using concentrations from Run 1, show that the concentration of NaOH has changed insignificantly when half of a CV chloride has been consumed?
Instructions

Data table
Instructions
Data table
1 Answer
The amount of NaOH reacted after one half-life is 0.02 % of the original.
Explanation:
Step 1. Calculate the initial concentration of CV
Your reaction beaker contained 15.00 mL of water, 5.00 mL of 0.05 mol/L NaOH, and 10.00 mL of the CV solution.
The reported values for the molar absorptivity of CV vary widely. The most precise value I found was
We can use Beer's Law to calculate the concentration of CV in the reaction mixture.
#color(blue)(bar(ul(|color(white)(a)A = epsilonclcolor(white)(a)|)))" "#
where
I assume that the path length of your cuvette was 1 cm. Then
Step 2. Calculate the initial moles of CV
Step 3. Calculate the initial moles of
After one half-life
The equation for the reaction is
#"CV"^"+" + "OH"^"-" → "CVOH"#

