Total Internal Reflection?
Could somebody please explain the entirety of Total Internal Reflection in regards to the CIE O level syllabus? I usually use miniphysics.com for help, but even their notes are too difficult for me to comprehend. Please help! Thanks!
Could somebody please explain the entirety of Total Internal Reflection in regards to the CIE O level syllabus? I usually use miniphysics.com for help, but even their notes are too difficult for me to comprehend. Please help! Thanks!
1 Answer
Snell's law helps to understand this.
Explanation:
Snell's law tells us how light behaves when it goes from one medium into another.
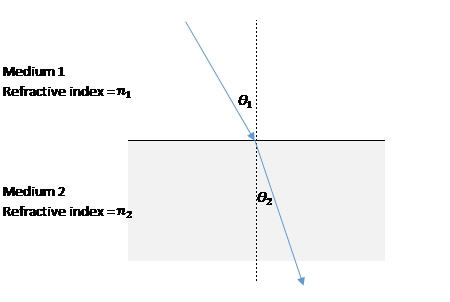
In the above, Snell's law tells us that :
If light is travelling from one medium to a medium with a lower refractive index (or put another way, from one medium to a less optically dense medium) then
By Snell's law then
If you increase the angle of incidence,
Beyond this, and the ray will be reflected - this is total internal reflection.
For example, if medium 1 is glass (
We can see that
hence
Hence when
If you try
And

