Trace the surface #x^2/4+y^2/9-z^2/4=1#. Also, describe its sections by the planes x=±2,algebraically and geometrically.?

Question

2490 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-01-28T14:03:50

See below.

The surface

#C(x,y,z)= x^2/4 + y^2/9 - z^2/4 - 1=0#

as well as the planes

#Pi_(1,2)->xpm 2# are represented in the attached figure.

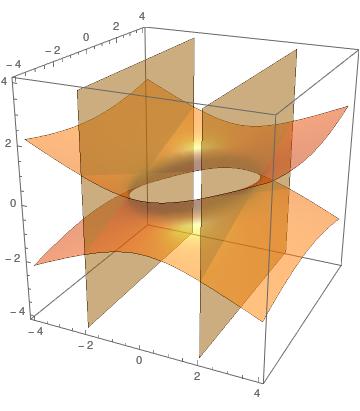
enter image source here

The trace #C nn Pi_(1,2)# are the lines

#C(-2,x,y)=0 rArr 1 +(y/3)^2-(z/2)^2-1=0 rArr (y/3-z/2)(y/3+z/2)=0#

and

#C(2,x,y)=0 rArr 1 +(y/3)^2-(z/2)^2-1=0 rArr (y/3-z/2)(y/3+z/2)=0#

or

#L_1 -> {(y=pm3/2 z),(x=-2):}#

#L_2 -> {(y=pm3/2 z),(x=2):}#