Question

Triangle A has an area of `15` and two sides of lengths `8` and `7`. Triangle B is similar to triangle A and has a side with a length of `14`. What are the maximum and minimum possible areas of triangle B?

Answer 1

Maximum possible area of triangle B = 60
Minimum possible area of triangle B = 45.9375

Explanation:

`Delta s A and B` are similar.

To get the maximum area of `Delta B`, side 14 of `Delta B` should correspond to side 7 of `Delta A`.

Sides are in the ratio 14 : 7
Hence the areas will be in the ratio of `14^2 : 7^2 = 196 : 49`

Maximum Area of triangle `B =( 15 * 196) / 49= 60`

Similarly to get the minimum area, side 8 of `Delta A` will correspond to side 14 of `Delta B`.
Sides are in the ratio `14 : 8` and areas `196 : 64`

Minimum area of `Delta B = (15*196)/64= 45.9375`

Answer 2

Maximum area: `~~159.5` sq. units
Minimum area: `~~14.2` sq. units

Explanation:

If `triangle_A` has sides `a=7`, `b=8`, `c=?` and an area of `A=15`
then `c~~4.3color(white)("XXX")"or"color(white)("XXX")c~~14.4`
(See below for indication of how these values were derived).

Therefore `triangleA` could have a minimum side length of `4.3` (approx)
and a maximum side length of `14.4` (approx.)

For corresponding sides:
`color(white)("XXX")("Area"_B)/("Area"_A)=(("Side"_B)/("Side"_A))^2`
or equivalently

`color(white)("XXX")"Area"_B="Area"_A * (("Side"_B)/("Side"_A))^2`

Notice that the greater the length of the corresponding `"Side"_A`,
the smaller the value of `"Area"_B`
So given `"Area"_A=15`
and `"Side"_B=14`
and the maximum value for a corresponding side is `"Side"_A~~14.4`
the minimum area for `triangleB` is `15 * (14/14.4)^2 ~~14.164`

Similarly, notice that the smalle the length of the corresponding `"Side"_A`,
the greater the value of `"Area"_B`
So given `"Area"_A=15`
and `"Side"_B=14`
and the minimum value for a corresponding side is `"Side"_A~~4.3`
the maximum area for `triangleB` is #15 * (14/4.3)^2 ~~159.546 #

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

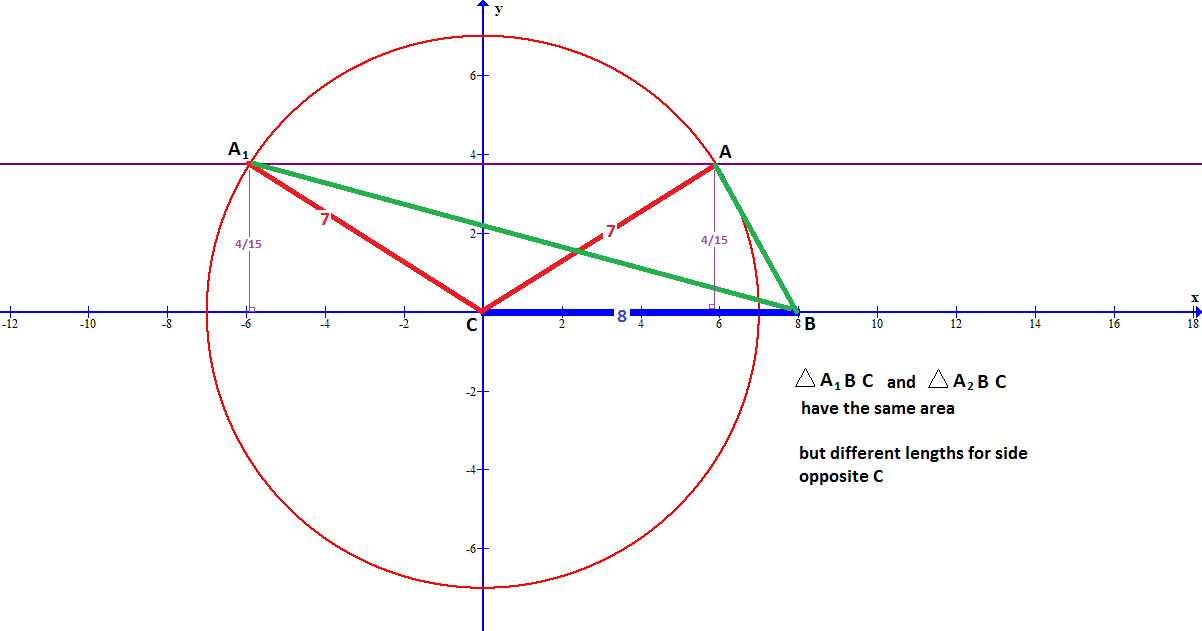
Determining possible lengths for `c`

Suppose we place `triangleA` on a standard Cartesian plane with the side with length `8` along the positive X-axis from `x=0` to `x=8`
Using this side as a base and given that the Area of `triangleA` is `15`
we see that the vertex opposite this side must be at a height of `y=15/4`

If the side with length `7` has one end at the origin (coterminal there with the side of length 8) then the other end of the side with length `7` must be on the circle `x^2+y^2=7^2`
(Note that the other end of the line of length `7` must be the vertex opposite the side with length `8`)

Substituting, we have
`color(white)("XXX")x^2+(15/4)^2=7^2`

`color(white)("XXX")x^2=559'16`

`color(white)("XXX")x=+-sqrt(559)/4`

Giving possible coordinates: `(-sqrt(559)/4,15/4)` and `(+sqrt(559)/4,15/4)`

We can then use the Pythagorean Theorem to calculate the distance to each of the points from `(8,0)`
giving the possible values shown above (Sorry, details missing but Socratic is already complaining about the length).