Triangle A has an area of #6 # and two sides of lengths #5 # and #3 #. Triangle B is similar to triangle A and has a side with a length of #14 #. What are the maximum and minimum possible areas of triangle B?
1 Answer
Explanation:
If
then the height of
(Since
and
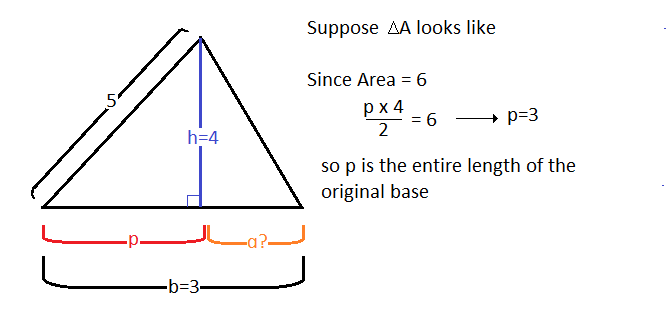
If
-
#B# 's maximum area will occur when the side of length#14# corresponds to#DeltaA# 's side of length#3#
In this case#DeltaB# 's height will be#4xx14/3=56/3#
and its area will be#(56/3xx14)/2=130 2/3# (sq. units) -
#B# 's minimum area will occur then the side of length#14# corresponds to#DeltaA# 's side of length#5#
In this case
#color(white)("XXX")B# 's height will be#4xx14/5=56/5#
#color(white)("XXX")B# 's base will be#3xx14/5=42/5#
and
#color(white)("XXX")B# 's area will be#(56/5xx42/5)/2=2352/50=4704/100=47.04# (sq.units)
