If we use the side of A with length #9# as the base
then the height of A relative to this base is #2#
(since the area of A is given as #9# and #"Area"_triangle=1/2xx"base"xx"height"#)
Note that there are two possibilities for #triangleA#:
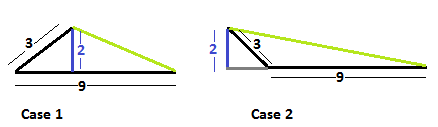
The longest "unknown" side of #triangleA# is obviously given by Case 2 where this length is the longest side possible.
In Case 2
#color(white)("XXX")#the length of the "extension" of the side with length #9# is
#color(white)("XXXXXX")sqrt(3^2-2^2)=sqrt(5)#
#color(white)("XXX")#and the "extended length" of the base is
#color(white)("XXXXXX")9+sqrt(5)#
#color(white)("XXX")#So the length of the "unknown" side is
#color(white)("XXXXXX")sqrt(2^2+(9+sqrt(5))^2)#
#color(white)("XXXXXXXX")=sqrt(90+18sqrt(5))#
#color(white)("XXXXXXXX")=3sqrt(10+2sqrt(5))#
The Area of a geometric figure varies as the square of its linear dimensions.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The maximum area of #triangleB# will occur when #B#'s side of length #7# corresponds to the shortest side of #triangleA# (namely #3#)
#("Area of "triangleB)/("Area of "triangleA)=7^2/3^2#
and since #"Area of "triangleA =2#
#rArr "Area of "triangleB = (7^2)/(3^2)xx2=98/9=10 8/9#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The minimum area of #triangleb# will occur when #B#'s side of length #7# corresponds to the longest possible side of #triangleA# (namely #3sqrt(10+2sqrt(5))# as shown above).
#("Area of "triangleB)/("Area of "triangleA)=7^2/((3sqrt(10+2sqrt(5)))^2)#
and since #"Area of "triangleA =2#
#rArr "Area of "triangleB = (7^2)/((3sqrt(10+2sqrt(5)))^2)xx2=98/(90+19sqrt(5))~~0.7524#

