Triangle A has an area of #9 # and two sides of lengths #4 # and #7 #. Triangle B is similar to triangle A and has a side with a length of #16 #. What are the maximum and minimum possible areas of triangle B?
1 Answer
Explanation:
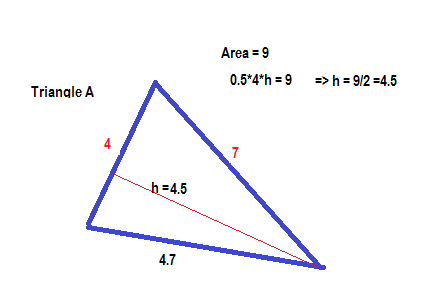
Given
If the angle between sides 4 & 9 be a then
Now if length of the third side be x then
So for triangle A
The smallest side has length 4 and largest side has length 7
Now we know that the ratio of areas of two similar triangles is the square of the ratio of their corresponding sides.
When the side of length 16 of triangle corresponds to the length 4 of triangle A then
Again when the side of length 16 of triangle B corresponds to the length 7 of triangle A then

