Triangle A has an area of #18 # and two sides of lengths #5 # and #9 #. Triangle B is similar to triangle A and has a side of length #12 #. What are the maximum and minimum possible areas of triangle B?
1 Answer
- Maximum possible are = 103.8
- Minimum possible area = 16.2
(but see note below)
Explanation:
We are given that in the triangle
Since the area of the triangle is 18 (see below), we know that the length of the altitude
Now, we can have either of the two situations depicted in the figure below
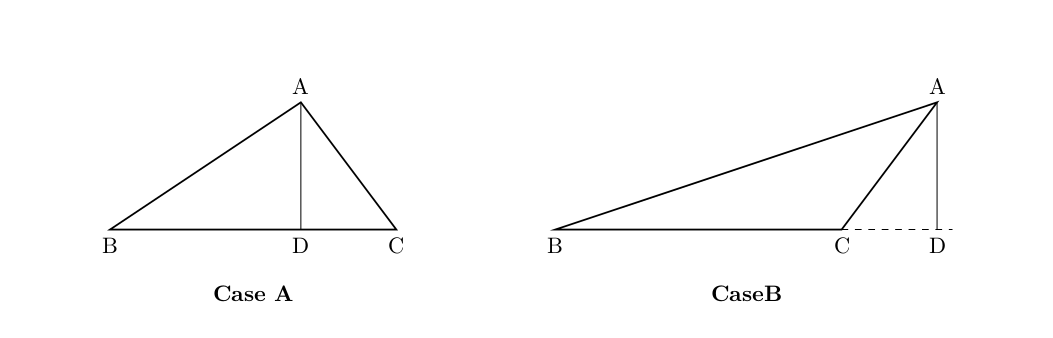
In either case,
In Case A :
In Case B :
Hence the side
Since
For the second triangle, the area will be the largest (resp. smallest) if the given side (of length 12)is its smallest (resp. largest) side.
Thus,
-
the smallest possible area is
#18 times (12/sqrt{160})^2 = 18times 12^2/160 = 16.2# -
the smallest possible area is
#18 times (12/5)^2 = 18times 12^2/5^2= 103.8#
Note
- The original problem quoted the area of the first triangle as 9. I have taken the liberty of changing it to 18 to ensure that the numbers come out nicer in the calculation. Of course, the same technique would work for the original data as well (giving, for example
#AD = 2# , leading to#BC = sqrt{5^2-2^2}=sqrt{21}# and so on) - The third side could also be found by solving the formula
#A = sqrt{s(s-a)(s-b)(s-c)},qquad s = (a+b+c)/2#
which would yield a quadratic for#c^2#

