Question

Trig Help Please?

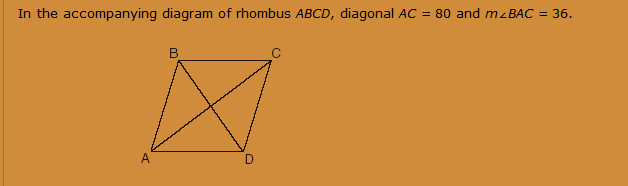(a) Find length of a side of the rhombus to the nearest tenth.
(b) Using your answer in part a, find the perimeter of rhombus ABCD.
(c) Find the length of diagonal (BD)to the nearest integer.

Answer 1

a) sides are all `49.4`

b) Perimeter `= 197.6`

c) `BD = 58`

Explanation:

Let's call the intersection of the diagonals point M,

Remember that in rhombus the diagonals bisect each other and intersect at 90°, so we have right angled triangles to work with.

In `DeltaBAM` we have: `hatA =36°, hatM = 90° and AM = 40`

a) With reference to `hatA, AM` is the adjacent side and `color(blue)(AB)` is the hypotenuse which is the length we need to know.

We can therefore use the Cos ratio `("adjacent"/"hypotenuse")`

`Cos36°=(AM)/(color(blue)(AB)) = 40/(AB)`

`color(blue)(AB) xxcos36° = 40`

`color(blue)(AB) = 40/cos36°`

`color(blue)(AB)= 49.4`

b) In a rhombus all the sides are equal, so now that we know the length of AB, the perimeter is `4 xx AB`

`P = 4 xx 49.4 = 197.6`

c) You can either use Pythagoras'theorem or trig to find the length of `BM` which will be doubled to give `BD`

`BM^2 = 49.4^2-40^2`

`BM^2 = 840.36`

`BM = sqrt840.36`

`BM = 28.98896`

`BD = 2 xx 28.98896`

`BD = 58`

Using trig is slightly more accurate because we use the original values, not arounded off value.

`(BM)/(AM) = tan36°`

`BM = 40tan36°`

`BM = 29.06`

`BD = 2 xx 29.06 = 58`

Answer 2

(a) Side `approx 49.4`; (b) Perimeter `approx 197.8`; (c) Diagonal `BD approx 58`

Explanation:

Using diagram in question.

Since `ABCD` is a rhombus `-> AB=BC=CD=AD`

(a) `:.triangle ABC` is isoceles `-> angle BCA = 36^o`

`:. angle ABC = 180 -72 = 108^o`

Applying the sine rule to `triangle ABC`

`80/sin108 = (BC)/sin 36`

`BC = (80sin36)/sin108`

`approx 49.44272 = 49.4` (1D)

(b) The four sides of a rhombus are equal.

`:.` Perimeter `approx 49.44272 xx4 = 197.8` (1D)

(c) Diagonal `BD` and diagonal `AC` bisect eachother at `90^o`

Let the point of intersection be `O`

`:. triangle BOC` is a right triangle.

Apply Pythagoras

`BO^2 + OC^2 = BC^2`

`BO^2approx 49.44272^2 -(80/2)^2`

`approx 844.582561`

`BO approx sqrt(844.582561) approx 29.06170`

But `BD = 2xxBO -> BD = 58` (0D)