Question

Two charged particles located at `(3.5, .5)` and `(−2, 1.5)`, have charges of `q_1 =3µC`, and `q_2=−4µC.` Find a) the magnitude and direction of the electrostatic force on q2? Locate a third charge `q_3= 4µC` such that the net force on `q_2` is zero?

Answer 1

`q_3` need to be placed at a point `P_3 (-8.34, 2.65)` about `6.45 cm` away from `q_2` opposite the attractive line of Force from `q_1 to q_2`. The magnitude of the force is `|F_(12)| = |F_(23)| = 35 N`

Explanation:

The Physics: Clearly `q_2` will be attracted toward `q_1` with Force, `F_e = k (|q_1||q_2|)/r^2` where
`k = 8.99xx10^9 Nm^2/C^2; q_1=3muC; q_2=-4muC`
So we need to calculate `r^2`, we use the distance formula:
`r = sqrt((x_2- x_1)^2 + (y_2-y_1)^2)`
`r = sqrt((-2.0- 3.5)^2 + (1.5-.5)^2)=5.59cm = 5.59xx10^-2 m`
`F_e = 8.99xx10^9 Ncancel(m^2)/cancel(C^2) ((3xx10^-6 * 4xx10^6)cancel(C^2))/((5.59xx10^-2 )^2 cancel(m^2))`
`color(red)(F_e = 35N)` as stated above `q_2` is getting pulled by `q_1`
the direction is given by the direction `q_2 -> q_1`
Thus the direction is:
`r_(12)=(x_1-x_2)i + (y_1 - y_2)j`
`r_(12)=(3.5-2.0)i + (05 - 1.5)j = 5.5i - j`
and the unit vector is: `u_(12) = 1/5.59(5.5i - j)`
and the direction angle: `tan^-1 -1/5.5 = -10.3^0`

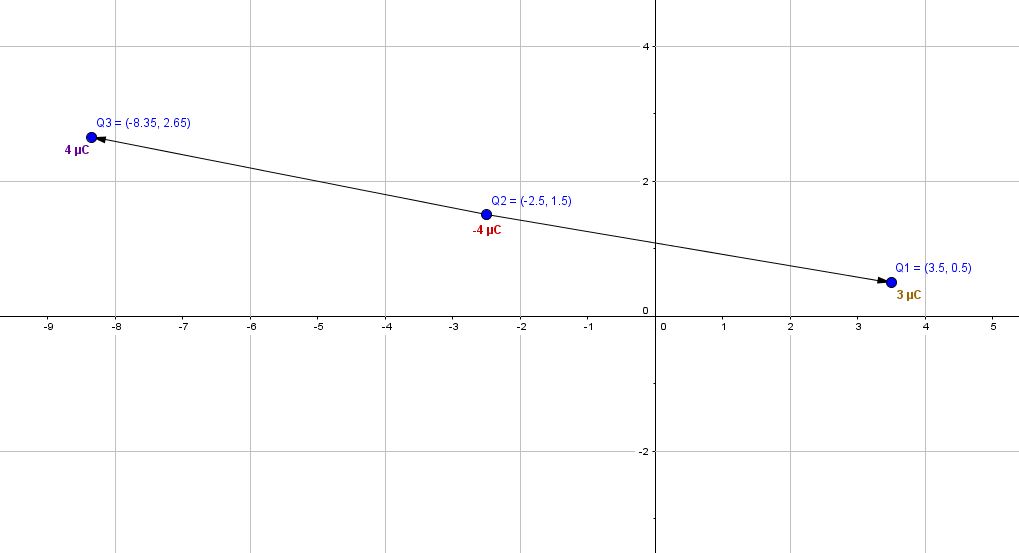
The 2nd question ask where should you place `q_3 = 4muC` so that the force on `q_2 = 0`

The Physics: Given that `q_2` is been pulled toward `q_1` we need a force opposite that. Now since `q_3` is positively charged the a Force that pulled in the opposite direction will be obtained by placing `q_3` on the line of force such that `q_2` somewhere between `q_3` and `q_1`.
We calculate `r_(23)` from the force equation knowing it is going to be `color(red)(F_e = 35N)`thus
`35=k(|q_2||q_3|)/r_(23)^2; r_(23)^2=8.99xx10^9 cancel(N)m^2/cancel(C^2) ((4xx10^-6 * 4xx10^6)cancel(C^2))/(35cancel(N)) = 4.1xx10^-3m; r_(23) = 6.45xx10^-2m = 6.45 cm`
Now given the direction is opposite the angle we are looking for is:
`theta = 180^0-10.3^0 = 169.7^0`
`r_(23) = 6.45cos(169.7)i + 6.45sin(169.7)j`
`r_(23) = -6.34i + 1.15j`
Now add this to the coordinates of `q_2(-2, 1.5)`
and `q_3` coordinates are: #q_3 (-8.34, 2.65)