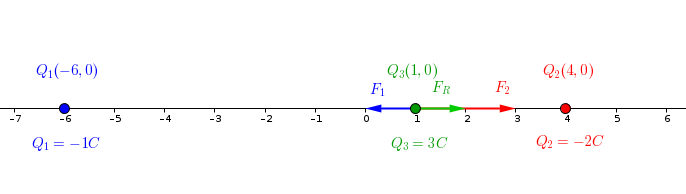
Two charges of # -1 C # and # -2 C# are positioned on a line at points # -6 # and # 4 #, respectively. What is the net force on a charge of # 3 C# at # 1 #?
1 Answer
May 14, 2016
Explanation: