Question

Two charges of `2 C` and `3 C` are positioned on a line at points `-5` and `6`, respectively. What is the net force on a charge of `-8 C` at `-2`?

Answer 1

Let us use Coulomb's Law for electrostatic interaction.

Explanation:

Charges distribution is given by this picture:

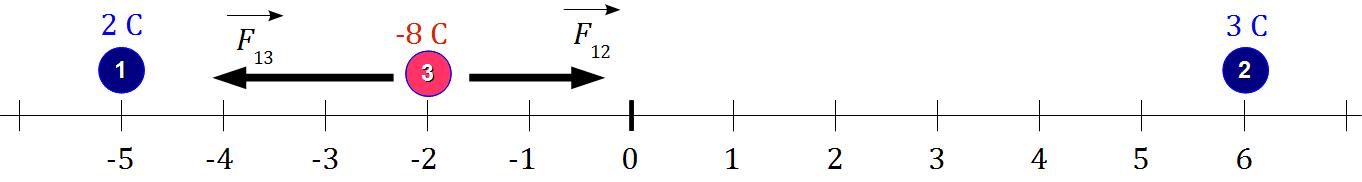
where blue charges will be our fonts, and the red charge will be our object charge.

According to Coulomb's Law, the force between two charges 1 and 2 is given by:

`F_{12} = {1}/{4 pi varepsilon_0} {q_1 cdot q_2}/{d^2} = K {q_1 cdot q_2}/{d^2}`

where `K = 9 cdot 10^9 "N" cdot "m"^2 / "C"^2` is electrostatic constant, `q_1` and `q_2` are the values of charges in coulombs, and `d` is the distance between both charges.
Electrostatic force is repulsive if both charges have the same sign, and attractive if they have opposite signs.

Let us calculate both forces:

• Force from 1 to 3:

`F_{13} = 9 cdot 10^9 "N" cdot "m"^2 / "C"^2 cdot {2 "C" cdot (-8) "C"}/(3 "m")^2 = -16 cdot 10^9 "N"`

• Force from 2 to 3:

`F_{23} = 9 cdot 10^9 "N" cdot "m"^2 / "C"^2 cdot {3 "C" cdot (-8) "C"}/(8 "m")^2 = -3,375 cdot 10^9 "N"`

Both forces are attractive (that's why both signs are negative). We must substract them, and the resultant force has the same orientation than the bigger one:

`F_"Total" = (16 cdot 10^9 "N") - (3,375 cdot 10^9 "N") = 12,625 cdot 10^9 "N"`

`vec F_"Total"` goes from charge 3 to charge 1 (because `F_{13}` is bigger than `F_{23}`)