Question

Two charges of `2 C` and `-3 C` are positioned on a line at points `-9` and `2`, respectively. What is the net force on a charge of `4 C` at `-2`?

Answer 1

`F_3=8.219*10^9N`

Explanation:

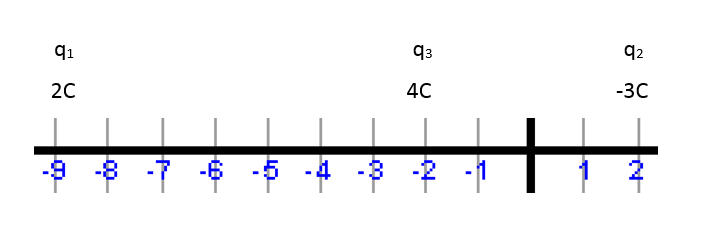
Consider the figure. Let the charges `2C, -3C` and `4C` be denoted by `q_1,q_2` and `q_3` respectively.
Let the positions at which charges are placed be in the units of meters.

Let `r_13`be the distance between the charges `q_1 and q_3`.
From figure
`r_13=-2-(-9)=-2+9=7 m`

Let `r_23`be the distance between the charges `q_2 and q_3`.
From figure
`r_23=2-(-2)=2+2=4 m`

Let `F_13` be the force due to charge `q_1` on the charge `q_3`
`F_13=(kq_1q_3)/r_13^2=(9*10^9*(2)(4))/7^2=1.469*10^9N`
This force is repulsive and is towards charge `q_2`.

Let `F_23` be the force due to charge `q_2` on the charge `q_3`
`F_23=(kq_2q_3)/r_23^2=(9*10^9*(3)(4))/4^2=6.75*10^9N`

This force is attractive and is towards charge `q_2`.

The total force or net force on charge `q_3` is the sum of above two forces.
Since the above two forces `F_13` and `F_23` are in same direction therefore they can be added directly.
Let `F_3` be the total force on the charge `q_3`.
`implies F_3=F_13+F_23=1.469*10^9+6.75*10^9=8.219*10^9N`
`implies F_3=8.219*10^9N`
Since `F_13 and F_23` are toward the charge `q_2` therefore the force `F_3` is also toward the charge `q_2`.