Two charges of # 3 C # and # -7 C# are positioned on a line at points # 6 # and # 5 #, respectively. What is the net force on a charge of # 2 C# at # -2 #?
1 Answer
#vecF_(n e t)=1.12xx10^10# #N#
Explanation:
The force between two charges is given by Coulomb's law:
#|vecF|=k(|q_1||q_2|)/r^2# where
#q_1# and#q_2# are the magnitudes of the charges,#r# is the distance between them, and#k# is a constant equal to#8.99xx10^9Nm^2//C^2# , sometimes referred to as Coulomb's constant.
Here is a quick diagram of the situation:

To find the net force on the
#vecF_(n e t)=sumvecF=vecF_(2 on 1)+vecF_(3 on 1)#
Recall that like charges repel, while opposite charges attract. Therefore, the force vectors can be drawn in as follows:
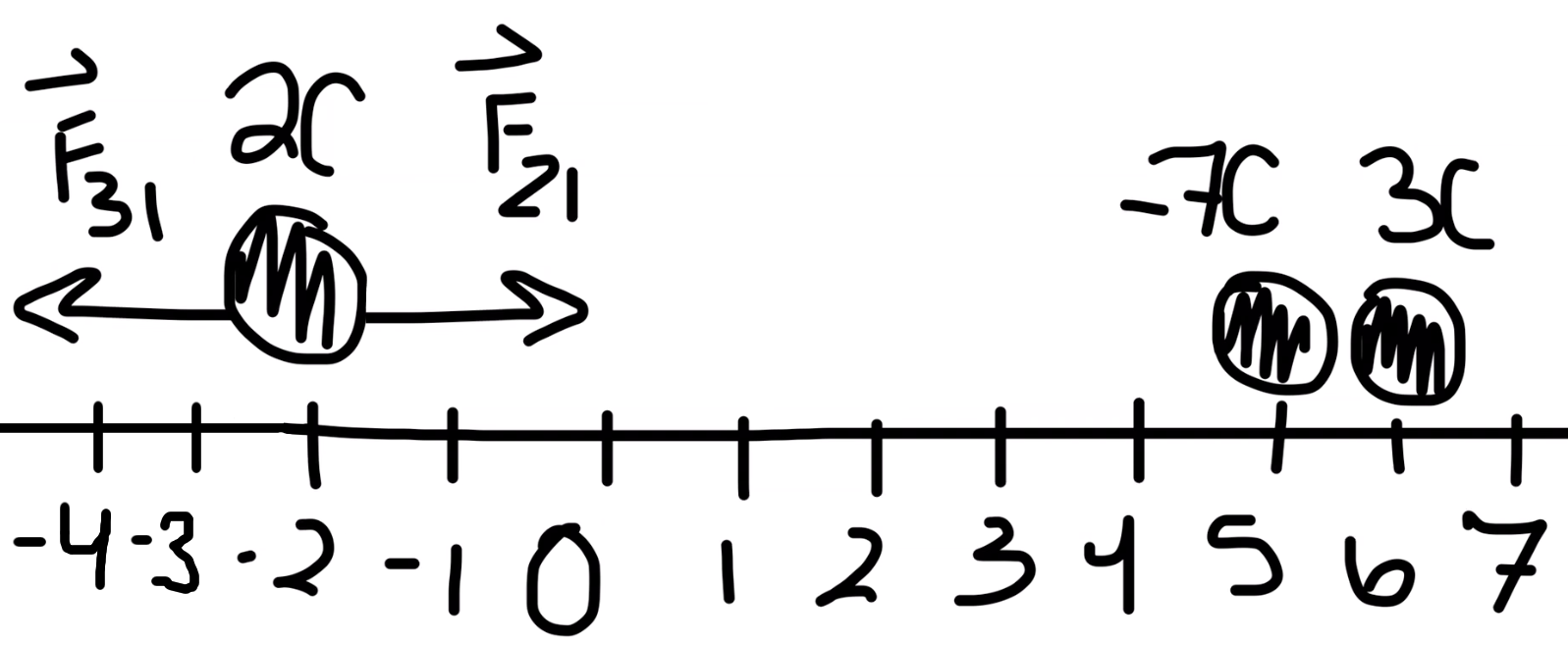
So we can calculate
#|vecF_(21)|=k*(|q_1||q_2|)/(r_(21)^2)#
#=(8.99xx10^9Nm^2//C^2)*(7C*2C)/(7)^2#
#=2.57*10^9# #N#
#|vecF_(31)|=k*(|q_1||q_3|)/(r_(31)^2)#
#=(8.99xx10^9Nm^2//C^2)*(3C*2C)/(8)^2#
#=8.43*10^8# #N#
Therefore, we have:
#vecF_(n e t)=1.73*10^9# #N#

