Two charges of # -4 C # and # -3 C# are positioned on a line at points # -8 # and # 16 #, respectively. What is the net force on a charge of # 2 C# at # -1 #?
1 Answer
Dec 24, 2015
No units are given for distance so I have assumed they are in metres for which:
Explanation:
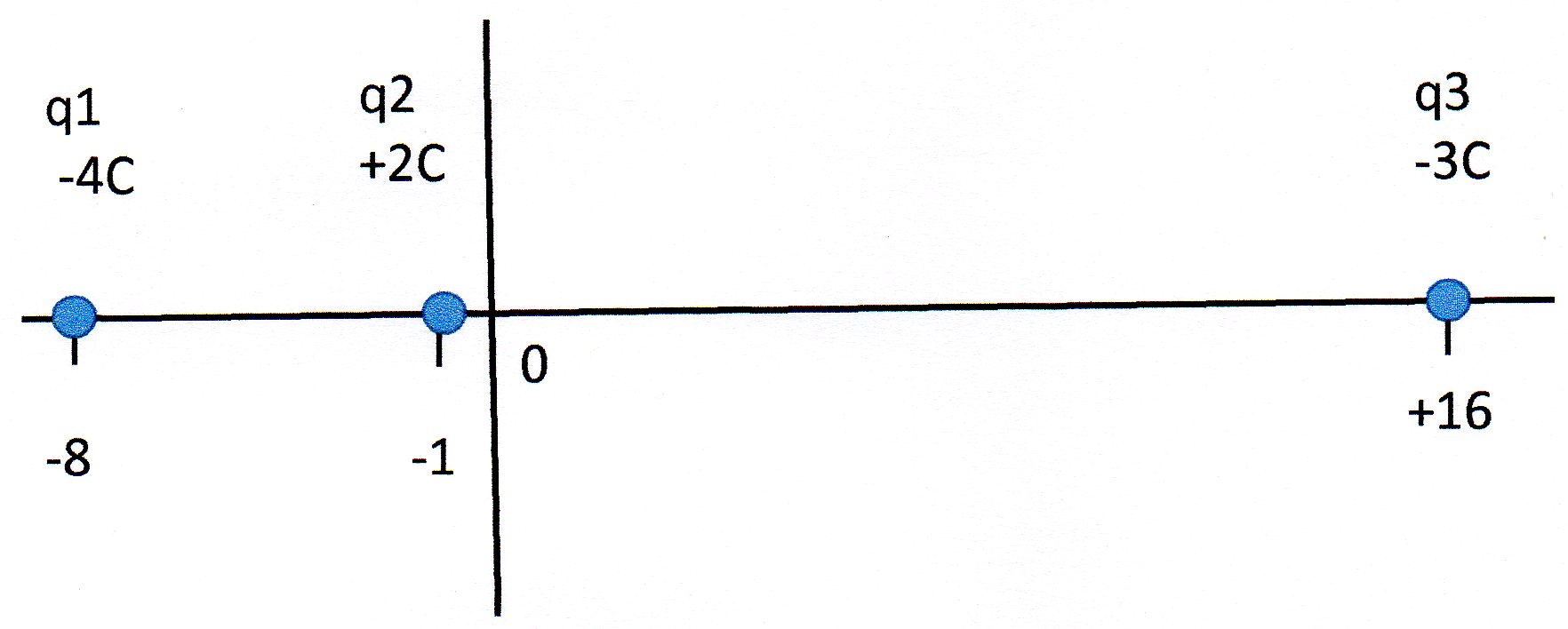
The force between two charges
This simplifies down to:
The net force on
The size of the force reflects how large a unit the coulomb is.

